8.9. Интегралы от неограниченных функций

Пусть функция непрерывна, а в точкеона имеет разрыв второго рода, так как(рис. 34).

В этом случае также не может быть вычислен по определению как предел интегральных сумм: вблизи точки, а, поэтому становится неопределённым поведение произведения. Но

функция непрерывна на отрезке, следовательно, существует(рис. 34), и величина этого интеграл зависит от. Тогда естественно сформулировать следующее определение.

ОПРЕДЕЛЕНИЕ. Если существует конечный , то он называетсянесобственным интегралом рода от неограниченной нафункции.

В этом случае говорят, что несобственный интеграл сходится (существует), и полагают, что .

Если этотпредел не существует или бесконечен, то несобственный интеграл рода называетсярасходящимся. В этом случае определенного численного значения ему не приписывается.

Аналогично, если функция непрерывнаи, то есть в точкеимеется разрыв второго рода (рис. 35), то , если этот предел существует и конечен. В этом случае говорят, что несобственный интеграл сходится.

у	Если же функция имеет разрыв второго рода в точке, а в остальных точкахона непрерывна (рис.36), то по определению полагают, что , причем называется

сходящимся, только если оба интеграла исходятся.

Таким образом, (рис 36).

Если хотя бы один из этих пределов бесконечен или не существует, то несобственный интеграл называется расходящимся.

ПРИМЕР. Вычислить несобственный интеграл (или установить его расходимость) .

Этот интеграл был рассмотрен ранее (см. п. 8.3) как иллюстрация невозможности применения формулы Ньютона-Лейбница для вычисления интеграла от разрывной функции. Так как – точка разрыва второго рода для функции, то– несобственный интеграл второго рода и по определению (рис. 37)

.

Но , поэтому данный интеграл расходится и никакого определенного численного значения ему приписать нельзя.

ПРИМЕР. Вычислить несобственные интегралы (или установить их расходимость): а) ; б);в).

а) интеграл сходится.

б) интеграл расходится.

в) интеграл расходится, так как .

Можно показать (сделайте это самостоятельно), что

(8.13)

и

(8.14)

Бесконечные пределы интегрирования или точки разрыва второго рода называются особенностями несобственных интегралов.

Для несобственных интегралов второго рода признаки сравнения сходимости справедливы в той же формулировке, что и для интегралов первого рода. Очень часто в качестве интеграла, с которым сравнивается данный несобственный интеграл, берут (8.13) или (8.14).

ПРИМЕР. Исследовать на сходимость .

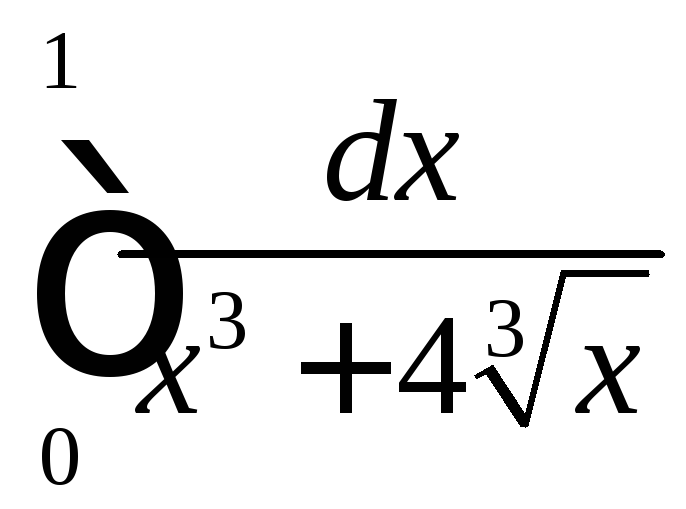В точке функцияимеет разрыв второго рода, значит, данный интеграл – несобственный интеграл второго рода. Для всехсправедлива оценка:– исходится ((8.13),). Следовательно, данный интеграл сходится по признаку сравнения.

Следует обратить внимание на различия в выборе подходящей функции для сравнения сходимости этого интеграла и несобственного интеграла первого рода от этой же функции (п. 8.8.).

ПРИМЕР. Исследовать на сходимость .

Этот интеграл имеет 2 особенности: – точку разрыва второго рода подынтегральной функции и бесконечный верхний предел интегрирования. Поэтому воспользуемся аддитивностью:

.

Исследуем каждый из несобственных интегралов по отдельности.

–подынтегральная функция. Первый интеграл является несобственным интегралом второго рода: он имеет особенность в точке , и при, близких к,, так как из всех слагаемых знаменателя при– самое большое. Таким образом,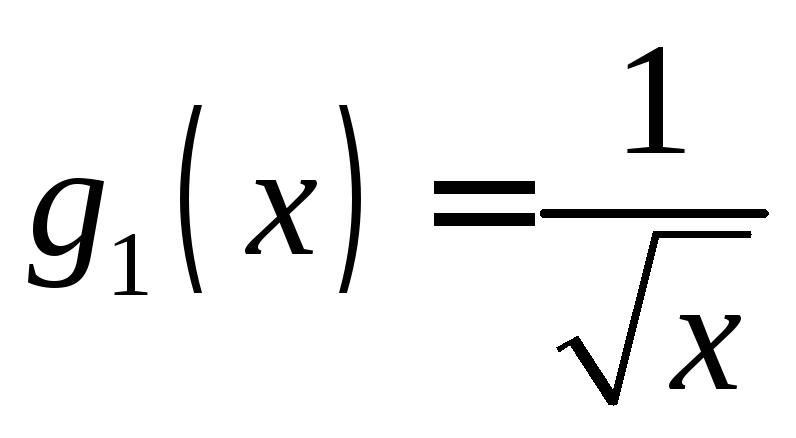– функция для сравнения сходимости в этом случае. Убедимся, что она выбрана верно, для чего найдем

.

Полученный предел конечен и не равен нулю, кроме того, сходится ((8.13),), значит,сходится по предельному признаку сравнения.

Рассмотрим второе слагаемое . Это несобственный интеграл первого рода с бесконечным верхним пределом. При достаточно больших, поэтому теперь функцией для сравнения будет.

Найдем (см.гл. 4). Так как найденный предел не равен нулю и конечен, то и эта функция выбрана верно, кроме того,сходится ((8.12),), значит,тоже сходится по предельному признаку сравнения. Отсюда следует, что исходныйсходится.

Отметим, что если б хотя бы один из двух исследованных интегралов расходился, то исходный интеграл был бы расходящимся.

64