8.8. Исследование сходимости несобственных интегралов с помощью признаков сравнения

Сформулируем без доказательства теоремы, позволяющие, не находя первообразной, сделать заключение о сходимости или расходимости несобственного интеграла.

ТЕОРЕМА (признак сравнения сходимости несобственных интегралов).

Пусть неотрицательные функции непрерывны, кроме того,. Тогда

1. если сходится , то сходится и;

2. если расходится , то расходится и.

Геометрический смысл этой теоремы ясен из рис. 33: сходимость несобственного интеграла означает, что площадь неограниченной области между графиком функциии осьюконечна, поэтому, если большая площадь конечна, то меньшая конечна и подавно. Также, если меньшая площадь бесконечна, то большая бесконечна тоже.

В качестве интеграла, с которым сравнивается исследуемый несобственный интеграл, часто выбирают .

ПРИМЕР. Исследовать на сходимость несобственный интеграл

.

Очевидно, что и, при этомсходится: см. (8.12) при. Таким образом, больший интегралсходится, значит, меньшийпо признаку сравнения тоже сходится.

Однако, для данной подынтегральной функции справедлива и такая оценка:

на промежутке , причёмрасходится ((8.12),). Понятно, что в таком случае нельзя сделать никакого заключения о поведении данного интеграла: если больший интегралрасходится, то меньший, может быть и сходящимся, и расходящимся.

Это означает, что при исследовании поведения несобственного интеграла с помощью признака сравнения важно правильно сделать оценку подынтегральной функции и правильно выбрать функцию для сравнения.

Часто это бывает сделать не очень просто. Поэтому во многих случаях удобней пользоваться другой теоремой.

ТЕОРЕМА (предельный признак сравнения сходимости несобственных интегралов). Пусть неотрицательные функции непрерывныи существуетконечный . Тогда несобственные интегралыисходятся или расходятся одновременно.

ПРИМЕР. Исследовать на сходимость несобственный интеграл

.

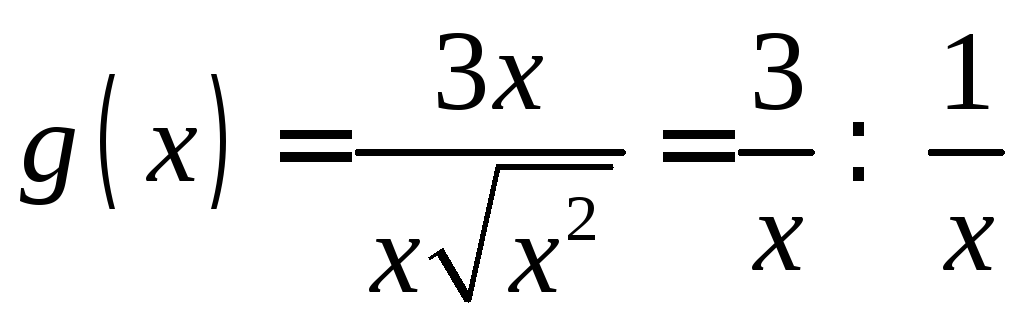По условию . Выберем функцию для сравнения: так как, то отбросим в числителе и знаменателе этой дроби слагаемые, несущественные при очень больших значениях. Тогда получим, арасходится ((8.12),).

Вычислим (см. гл.4). Полученный предел конечен, значит, данный интеграл ведет себя так же, как и интеграл, выбранный для сравнения, то есть расходится.

Рассмотрим еще раз предыдущий пример.

ПРИМЕР. Исследовать на сходимость несобственный интеграл

.

По условию . При больших значенияхповедение знаменателя определяется слагаемым, поэтому– функция для сравнения. Найдем. Так каксходится, то данный интеграл сходится тоже по предельному признаку сравнения.

ЗАМЕЧАНИЕ. Если окажется нулевым или бесконечным, это будет означать, что функция для сравнения выбрана неверно.

Предельным признаком сравнения сходимости очень удобно пользоваться, если подынтегральная функция представляет собой отношение степенных функций. Если же она содержит, например, показательную функцию, то чаще всего результат можно получить лишь с помощью признака сравнения.

ПРИМЕР. Исследовать на сходимость несобственный интеграл .

Так как числитель дроби при увеличениирастёт быстрее знаменателя, то естественно предположить, что этот интеграл расходится. Исходя из этого предположения, сделаем такую оценку подынтегральной функции: при. Вследствие того, чторасходится ((8.12),), данный интеграл также расходится по признаку сравнения.

ЗАМЕЧАНИЕ. Для несобственных интегралов ипризнаки сравнения сходимости формулируются и применяются аналогично.

Подчеркнем, что эти теоремы верны лишь для функций, неотрицательных (или не меняющих знак) на промежутке интегрирования.

ОПРЕДЕЛЕНИЕ. Пусть непрерывная функция меняет знак на. Тогда несобственный интегралназываетсяабсолютно сходящимся, если сходится 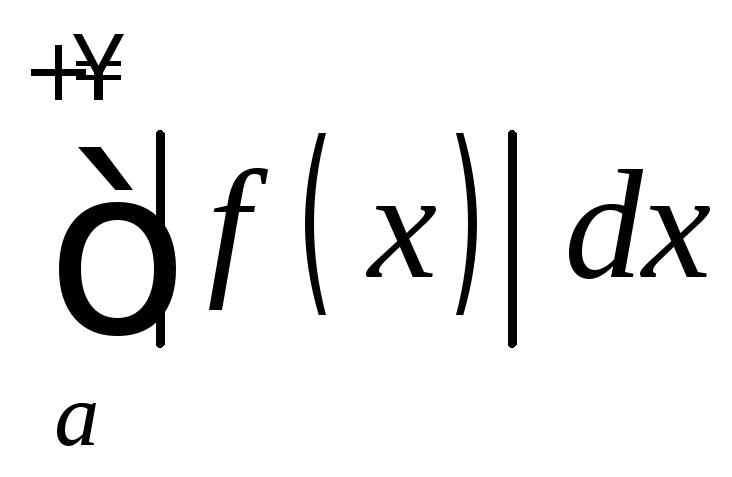. Если жесходится, арасходится, тоназываетсяусловно сходящимся.

Можно доказать, что абсолютно сходящийся несобственный интеграл сходится.

ПРИМЕР. Исследовать на сходимость несобственные интегралы

а) , б).

Заметим, что в обоих случаях подынтегральные функции меняют знак на промежутке интегрирования.

а)

, но не существует (см. гл. 4), значит, интеграл расходится.

б) Функция непрерывна при, но не имеет элементарной первообразной, поэтому исследовать сходимость этого интеграла, как предыдущего, непосредственно по определению невозможно.

Рассмотрим . Подынтегральная функция в этом интеграле неотрицательна и, так как. Кроме того, интегралсходится(8.12. ), следовательно, также сходится по признаку сходимости, а это означает, чтосходится абсолютно.