8.7. Несобственные интегралы. Интегралы с бесконечными пределами интегрирования

До сих пор при рассмотрении определенного интеграла мы считали, что отрезок интегрирования конечен, а подынтегральная функция непрерывна, или кусочно-непрерывна, но во всяком случае, ограничена.

Такие интегралы называются интегралами в собственном смысле слова, или собственными и по определению .

Если хотя бы одно из этих двух условий не выполнено, то есть

1. отрезок бесконечен, или

2. функция имеет наразрывII рода и по этой причине не является ограниченной,

то интеграл называется несобственным. Собственный интеграл всегда имеет определенное значение. В отличие от него несобственные интегралы не все имеют такое значение.

Рассмотрим первый случай: пусть непрерывная функция задана, причем. Тогда, с одной стороны, интеграл от этой функ-

ции на можно трактовать как площадь бесконечной криволинейной трапеции, а с другой, он не может быть вычислен по определению: при любом конечном разбиениипоследний из отрезковимеет бесконечную длину, значит, в интегральной сумме нельзя перейти к пределу при.

Но непрерывна, поэтомусуществует. Этот интеграл численно равен площади криволинейной трапеции (рис. 30), а величина его зависит от. Если сдвигатьнеограниченно вправо, то величина интеграла будет меняться, либо неограниченно возрастая, либо оставаясь ограниченной.

ОПРЕДЕЛЕНИЕ. Если существует конечный , то он называетсянесобственным интегралом рода (с бесконечным верхним пределом) от функции.

В этом случае говорят, что несобственный интеграл с бесконечным верхним пределом сходится (существует), и полагают, что

.

Если этот предел не существует или бесконечен, то несобственный интеграл называется расходящимся. В этом случае определенного численного значения ему не приписывается.

ЗАМЕЧАНИЕ. Из определения следует, что сходимость несобственного интеграла означает возможность замены определенного интеграла при больших (и часто не вполне известных) значенияхна несобственный интеграл.

ПРИМЕР. Вычислить несобственные интегралы (или установить их расходимость): а) , б).

х	а) интеграл расходится. б) интеграл сходится. Из рассмотренного примера следует, что площадь фигуры, ограниченной линиями (рис. 31) бесконечна.

Интересно, что объем тела, образованного вращением этой фигуры вокруг оси , конечен:.

Несобственный интеграл рода с бесконечным нижним пределом интегрирования от функции, непрерывной на, определяется аналогично.

ОПРЕДЕЛЕНИЕ. Если существует конечный 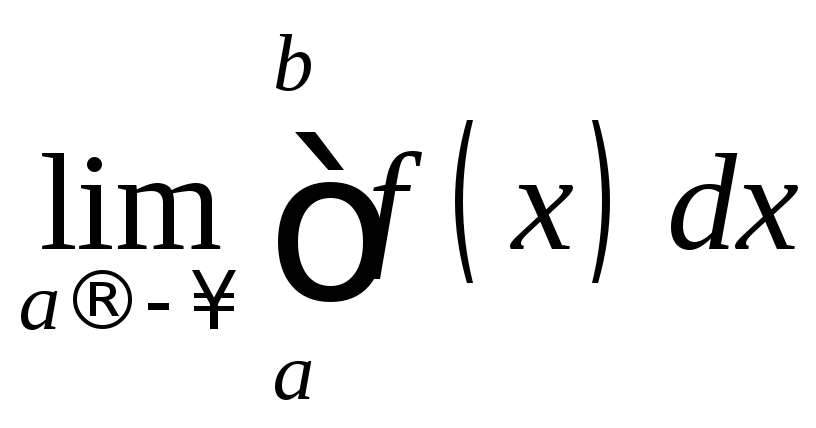, то он называетсянесобственным интегралом рода (с бесконечным нижним пределом) от функции.

В этом случае говорят, что несобственный интеграл с бесконечным нижним пределом сходится, и полагают, что . В противном случае несобственный интеграл называетсярасходящимся.

Кроме того, по определению полагается, что если функция непрерывна, то, где– произвольная фиксированная точка оси. Такой интегралсходится, если сходятся оба несобственных интеграла в правой части равенства. Если хотя бы один их них расходится, то интеграл по определению считаетсярасходящимся.

Можно показать, что большинство основных свойств определенных интегралов сохраняется для сходящихся несобственных интегралов с бесконечными пределами интегрирования. Сформулируем некоторые из них.

1. Если функция непрерывнаи сходится интеграл, то сходится также ии наоборот. При этом

.

2. Из сходимости интегралов иследует и сходимость интеграла,

причем .

Обратное утверждение неверно.

ПРИМЕР. Вычислить несобственный интеграл (или установить его расходимость) .

По определению

интеграл расходится, так как .

Заметим, что подынтегральная функция – нечетная, но пользоваться свойствами определенного интеграла по симметричному отрезку от четных или нечетных функций для вычисления несобственного интеграла можно, лишь если он сходится.

В данном случае интеграл расходится, и потому, несмотря на симметрию графика функции (рис. 32),не равен нулю.

ПРИМЕР. Исследовать на сходимость несобственный интеграл при различных значениях.

При интеграл, как уже было показано, расходится.

При .

Если , тосходится по определению. В этом случае.

Если же , тоинтеграл расходится по определению. Итак,

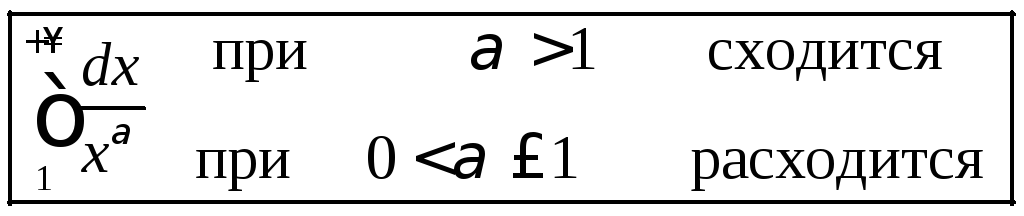(8.12)

ЗАМЕЧАНИЕ. Для сходящихся несобственных интегралов справедлива формула интегрирования по частям и теорема о замене переменной в определённом интеграле.

ПРИМЕР. Найти путь, пройденный от начала движения до полной остановки телом, если его скорость м/сек.

Как известно, если скорость движения непостоянна, то путь, пройденный телом за время , находится по формуле:.

В нашем случае . Но ни при каком значениискорость движения не обращается в ноль. Однако, функция(см.гл. 4), а это означает, что при некоторомдостаточно большом, но точно не известном значении времени скорость станет настолько мала, что тело можно будет считать остановившимся.

Как было отмечено выше, сходимость несобственного интеграла означает возможность замены определенного интеграла при большом (и не вполне известном) значениина несобственный интеграл.

Поэтому

.

Полученный конечный результат означает, что интеграл сходится. Кроме того, при вычислении имелось в виду, что

.

ПРИМЕР. Вычислить несобственный интеграл (или установить его расходимость) .

Сделаем замену переменной по формуле: ;

.

Отсюда

.

Отметим, что после этой замены несобственный интеграл стал определённым.