2.3. Метод наименьших квадратов

В задачи экспериментальной физики входит не только измерение конкретных величин, но и исследование зависимостей между физическими характеристиками.

Пусть в результате эксперимента получен ряд значений величины  , соответствующих значениям аргумента , и необходимо построить график зависимости .

Характер теоретической зависимости обычно бывает известен из физического смысла задачи (например, зависит от по линейному или квадратичному закону). Однако экспериментальные точки вследствие неизбежных погрешностей, возникающих при измерениях, имеют разброс относительно ожидаемой графической зависимости.

Задача экспериментатора − провести по экспериментальным точкам линию, которая давала бы наилучшее согласие между экспериментальными результатами и теоретической зависимостью  .

Для решения подобных задач применяется метод наименьших квадратов (МНК).

Ограничимся случаем, когда ожидаемую зависимость между и можно полагать линейной. Тогда функция записывается в следующем виде:

. (21)

В основе МНК лежит положение, согласно которому наилучшим приближением к теоретической будет такая прямая линия, для которой сумма квадратов разностей экспериментальных значений и соответствующих вычисленных значений является минимальной.

То есть наиболее вероятные значения параметров и выбирают так, чтобы сумма была минимальной:

.

Условие минимума выполняется, если равны нулю частные производные и :

,

.

Записанные соотношения являются системой линейных алгебраических уравнений:

, (22)

. (23)

Решение системы уравнений (22) и (23) приводит к следующим значениям искомых параметров и :

, (24)

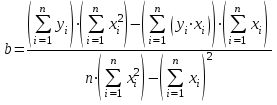. (25)

Примечание. Значения параметров и не изменится, если ввести в (24) и (25) другие переменные:

; ,

где и определяются соответственно как

,  ,

однако расчетные формулы и при этом упрощаются:

, (26)

. (27)

Коэффициенты, вычисленные по формулам (24) и (25) или (26) и (27), полагаются наилучшими приближенными значениями (оценками) параметров и линейной функции (21). Их значения можно использовать для вычисления при произвольных значениях аргумента .

В тех случаях, когда до опыта известно, что зависимость проходит через начало координат, т.е. ожидаемую зависимость можно представить в виде

, (28)

значение параметра , согласно МНК, находят из условия минимума суммы:

. (29)

Дифференцируя (29) по параметру и приравнивая нулю, получаем:

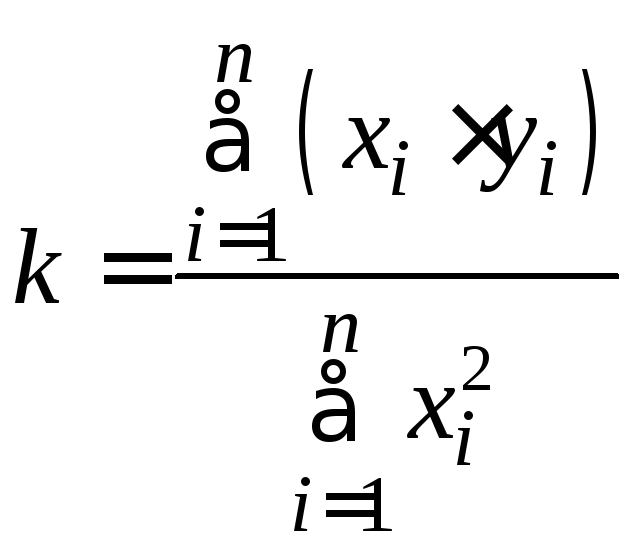. (30)

Рассчитанное по формуле (30) значение параметра является наилучшим в функциональной зависимости .

Метод наименьших квадратов дает не истинные параметры и в линейной зависимости , а их наиболее вероятные приближённые значения. Следовательно, при построении искомой прямой линии, аппроксимирующей экспериментальную зависимость, кроме значений параметров и , необходимо в общем случае знать и доверительные интервалы, в которых они лежат. Для этого требуется оценить среднеквадратичные погрешности, с которыми и определены.

Математическая статистика даёт следующие выражения для среднеквадратичных погрешностей параметров и :

, (31)

. (32)

В частном случае, когда прямая проходит через точку , , вычисляют среднеквадратичную погрешность определения только параметра :

. (33)

Полуширину доверительного интервала, с которой определено значение параметра , вычисляют по стандартной методике:

, (34)

здесь – коэффициент Стьюдента для надежности и числа пар точек .

Пример. В эксперименте получено пять измерений величин и , результаты которых приведены в таблице. Известно, что уравнение измерения имеет вид  . Используя метод наименьших квадратов, рассчитать наилучшее значение коэффициента и погрешность  , с которой этот коэффициент определён. Построить наилучшую прямую.

Для наглядности сведём исходные данные и результаты расчетов в таблицу.

1 2 3 4 5	0,4 0,8 1,2 1,6 2,0	0,50 1,40 1,66 2,80 3,20	0,16 0,64 1,44 2,56 4,00	0,20 1,12 1,99 4,48 6,40	1,61	-0,144 0,112 -0,272 0,224 -0,020	0,0207 0,0125 0,0740 0,0502 0,0004	0,19

1)  По формуле (30) найдем величину параметра  :

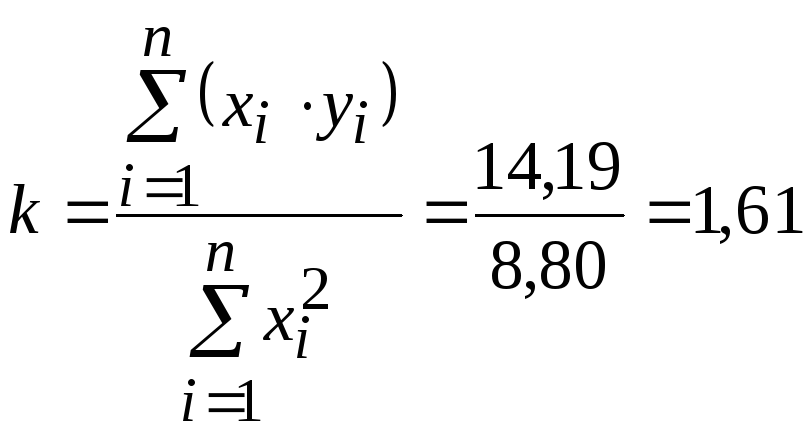
2)  По формуле (33) оценим среднеквадратичную погрешность определения параметра :

.

3)  Задаем значение доверительной вероятности . По таблице определяем значение коэффициента Стьюдента (при и ).

4)  По формуле (34) вычислим абсолютную погрешность определения параметра :

.

5)  Окончательный результат:

при доверительной вероятности .

6)  Запишем уравнение наиболее правдоподобной прямой:

.

7)  Поскольку зависимость  линейная, то для построения графика достаточно найти только одну точку и провести прямую через начало координат и найденную точку. Эта прямая (см. рис.) и будет "наилучшей" прямой, описывающей заданную функциональную зависимость.

Примечание.  Если экспериментальная зависимость заменяется аналитическим уравнением прямой линии, то при определении абсолютной погрешности величины , соответствующей значению аргумента , применяется метод переноса ошибок (см. 1.7). В частности, если прямая проходит через начало координат, абсолютная погрешность   равна:

,

где абсолютная погрешность определения параметра .