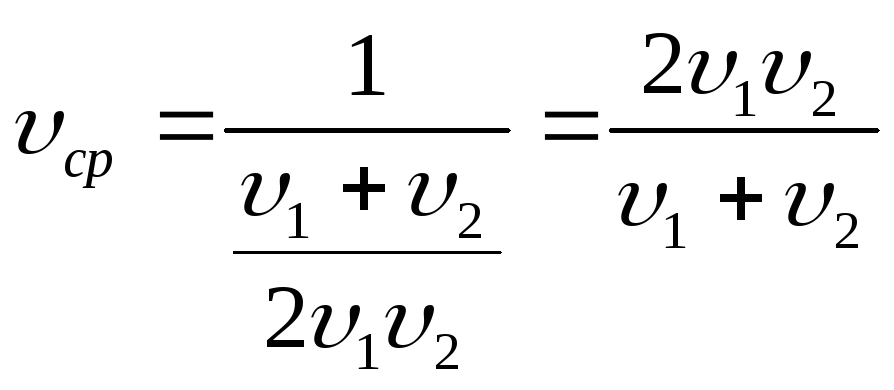2. Перемещение

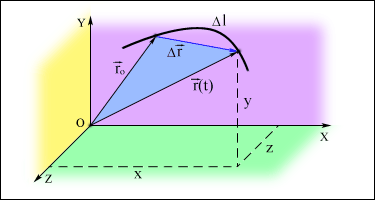
Перемещение

_{; (1.2)}

Модуль вектора перемещения

_(1.2)

Линия, которую описывает материальная точка, перемещаясь в пространстве, называется траекторией.

Путь - длина траектории, вдоль которой движется тело.

3. Скорость.

Скорость - является векторной величиной, которая определяет как быстроту движения, так и его направление в данный момент времени.

Средняя скорость это скорость тела расчитанная за относительно большой интервал времени

_{Пример.}

_{Определить среднюю скорость на всем пути, если первую половину пути тело двигалось со скоростью 72 км/ч, а вторую половину пути со скоростью 36 км/ч.}

	Си
	=20 м/с =10 м/с

Мгновенная скорость -скорость в данной точке траектории в данный момент времени.

_{; (1.2)}

Вектор мгновенной скорости для каждого момента времени направлен по касательной к траектории в сторону движения, т.е.

_{Мгновенная скорость по модулю}

_{; (1.2)}

Если выражение проинтегрировать в пределах отдо, то найдем длину пути, пройденного точкой за время:

_(1.2)

4. Ускорение

Ускорение- это физическая величина, характеризующая быстроту изменения вектора скорости.

Средним ускорением , называется векторная физическая величина, численно равная отношению изменения вектора скоростик промежутку времени, за которое это изменение произошло:

(1.2)

Направление  совпадает с направлением .

Мгновенным ускорением называют векторную величину, численно равную пределу, к которому стремится среднее ускорение за промежуток времени, при. Т.е. это ускорение в данной точке траектории

_(1.2)

Используя соотношение (1.12), получим:

_{. (1.2)}

Вектор мгновенного ускорения равен первой производной от вектора скорости по времени или второй производной от вектора перемещения по времени.

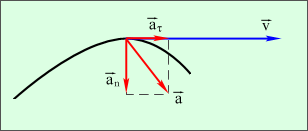
Тангенциальное ускорение - составляющее полного ускорения характеризующие изменение скорости по величине.

_(1.2)

Направление вектора совпадает с направлением касательной к траектории:

(Следует обратить внимание: полное ускорение = и тангенциальное ускорение _ = две разные физические величины).

Нормальное ускорение – составляющие полного ускорения, характеризующие изменение скорости по направлению.

Нормальная составляющая вектора , характеризует изменение ско­рости за время t по направлению.

Допустим, что точка В достаточно близка к точке А, поэтому s можно считать дугой окружности некоторого радиуса r, мало отличающейся от хорды АВ.

Тогда из подобия треугольников АОВ и EAD следует, что _, но т.к. , то

_(1.2)

При , стремится к нулю, а так как треугольник EAD равнобед­ренный, то угол ADE между истремится к прямому. Следовательно, привекторы итакже оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор , перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

_(1.2)

называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).

Соотношение для справедливо не только для плоского движения, но и для любого движения, только вместо радиуса окружностиr надо подставлять радиус кривизны траектории.

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих ускорения (рис. 1.6).

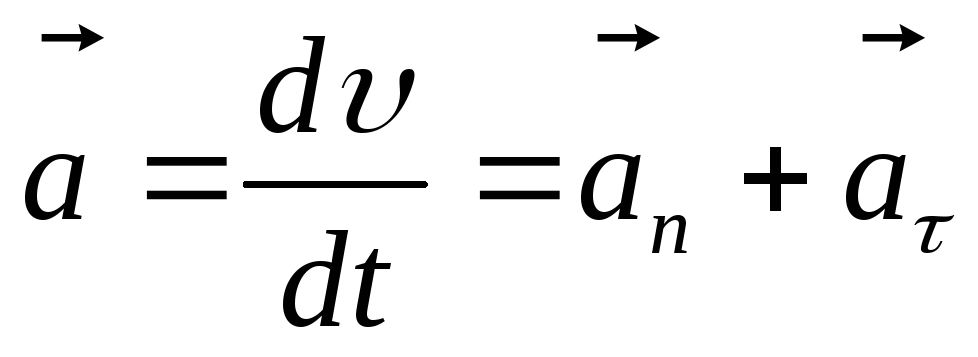_{; (1.2)}

Модуль ускорения можно определить по формуле:

_(1.2)

При равномерном движении по окружности тангенциальное ускорение отсутствует. Полное ускорение равно нормальному ускорению и направлено по радиусу окружности к ее центру. Поэтому нормальное ускорение часто называют центростремительным.

Прямолинейное равноускоренное/равнозамедленное движение

_(1.2)

_(1.2)