2. Стационарное течение жидкости. Уравнение неразрывности

Движение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком.

Абсолютно несжимаемая и абсолютно невязкая жидкость называется идеальной жидкостью.

Всю жидкость можно представить в виде поля вектора скорости. Тогда в поле вектора скорости можно провести линии, касательные к которым в каждой точке совпадают с направлением скорости частицы жидкости в этой же точке. Такие линии называются линиями тока жидкости (рис. 1.29). Линии тока приня­то проводить так, что густота их была бы больше там, где больше скорость течения жидкости, и меньше там, где жидкость те­чет медленнее.

Установившееся течение жидкости называют стационарным течением.

В случае стационарного течения скорость жидкости в любой точке объе­ма остается неизменной. Линии тока при стационарном течении остаются неизменными и совпадают с траекто­рией отдельных частиц жидкости.

Часть жидкости, ограниченную линиями тока, называют трубкой тока

Возьмем трубку тока и выберем два нормальных сечения S₁ и S₂ (рис. 1.29). Обозначим через скорость течения жидкости в том месте, где проведено сечениеS₁, — скорость в сеченииS₂. Тогда за е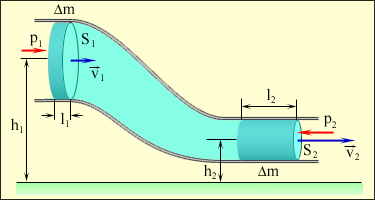диницу времени через сечениеS₁ пройдет объем жид­кости, равный , а через сечениеS₂ объем . Посколь­ку жидкость несжимаемая, то

_(1.2)

Это соотношение справедливо для любых двух сечений труб­ки тока. уравнением неразрывности для не­сжимаемой жидкости

_(1.2)

где - объемный расход.

По теореме о неразрывности струи в тех местах, где труба шире, жидкость будет протекать медленней, а в тех местах, где труба уже, скорость течения жидкости будет больше. Другим вы­водом является то, что давление в широких местах больше, чем в узких.

3. Уравнение Бернулли

При протекании некоторой массы жидкости m, будет совершаться механическая работа, т.к. на эту массу жидкости действует сила, обу­словленная наличием давления Р. По закону сохранения энергии

_{Е2 – Е1 = А}

_(1.2)

_;;

_(1.2)

Для переноса массы жидкости m в месте расположения первого сечения жидкость должна продвинуться на отрезок l₁ = ₁t, во втором сечении на отрезок .

Силы, дей­ствующие на оба конца выделенного участка жидкости, соответ­ственно равны

_и(1.2)

_{, (1.2)}

_(1.2)

Перепишем последнее уравнение в виде

_(1.2)

Согласно закону о неразрывности струи

где V - объем жидкости, заключенный между сечениями S₁ и S₂.

_(1.2)

Разделим на V

и, принимая во внимание, что плотность жидкости  = m/V, имеем

_(1.2)

т.к. сечения выбирались произвольно, то можем записать уравнением Бернулли

_(1.2)

Уравнение Бер­нулли — выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости.

Р -статическое давле­ние (давление жидкости на поверхность обтекаемого ею тела),

—динамическое давление.

gh -гидростатическое давле­ние.

Если трубка тока расположена горизонтально (h₁ = h₂), то уравнение Бернулли имеет следующий вид:

_(1.2)

_или

_{, (1.2)}

где – называется полным давлением.

4. Измерение давлений

5. Следствия из уравнения Бернулли

Трубка Вентури

_{, (1.2)}

т.к. , тои следовательно

_(1.2)

_{трубка Пито-Прандтля}

_{Р0 – Р = 0gh (1.2)}

где ₀ — плотность жидкости в манометре.

согласно уравнению Бернулли,

_(1.2)

Из формул (1.58) и (1.59) получаем искомую скорость пото­ка жидкости

_(1.2)

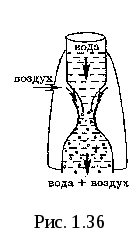
3. Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса рис.1.36.

Таким образом, можно откачивать воздух из сосуда до давления 100мм.рт.ст. (1 мм рт.ст. =133,32 Па)

4. Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Возьмем цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие (рис. 1.37). Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₂ выхода ее из отверстия). Напишем для них уравнение Бернулли

_(1.2)

Так как давление Р₁ и P₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т.е. Р₁ = P₂, то уравнение будет иметь вид

_(1.2)

Из уравнения неразрывности (1.62) следует, что .

где S₁ и S₂ - площади поперечных сечений сосуда и отверстия. Если S₁  S₂ то членом можно пренебречь и;

- это выражение получило название формулы Торричелли,

т.е. скорость истечения жидкости из отверстия (бокового или донного) равна скорости тела при свободном паде­нии его с высоты уровня жидкости. Эта скорость не зависит ни от плотности жидкости, ни от давления.