
- •Содержание
- •Основы молекулярной физики
- •Введение
- •Основные понятия
- •1. Идеальным газом, называется газ, подчиняющийся следующим условиям:
- •Основное уравнение молекулярно-кинетической теории газов.
- •Уравнение состояния идеального газа
- •Изопроцессы в газах.
- •Закон Дальтона
- •Распределение молекул идеального газа, по скоростям и энергиям теплового движения
- •Максвелловское распределение по скоростям.
- •VВ (наиболее вероятная скорость)
- •Идеальный газ в силовом поле. Барометрическая формула
- •Закон Больцмана
- •Основы термодинамики
- •Общие понятия термодинамики
- •Закон равномерного распределения энергии по степеням свободы
- •Работа и теплота
- •Работа газа
- •Первый закон термодинамики
- •Применение первого начала термодинамики к изопроцессам.
- •Изобарный процесс.
- •Изохорный процесс
- •Изотермический процесс
- •Теплоемкость газов
- •Адиабатный процесс.
- •Состояние системы. Обратимые и необратимые процессы.
- •Круговые процессы (циклы)
- •Второе начало термодинамики
- •Цикл Карно
- •Термодинамическая шкала температур
- •Энтропия
- •3) Знак dS определяется q. Если q 0, система получает теплоту и изменение энтропии dS 0, т.Е. Энтропия возрастает. Если q 0, то dS 0 и энтропия системы убывает.
- •4) Энтропия замкнутой системы, совершающей обратимый цикл Карно, не изменяется.
- •5) Если система совершает необратимый процесс, то её энтропия возрастает. Действительно, для необратимых циклов , т.Е.
- •Свободная энергия
- •Энтальпия
- •Термодинамические потенциалы
- •Макроскопические параметры. Вероятность и флуктуации.
- •Энтропия и вероятность. Статистический смысл второго начала термодинамики
- •Гипотеза о «тепловой смерти» вселенной.
- •Реальные газы
- •Силы и потенциальная энергия межмолекулярного взаимодействия
- •Уравнение Ван-дер-Ваальса.
- •Учет собственного объема молекул.
- •Учет притяжения между молекулами.
- •График уравнения ван-дер-ваальса
- •Реальные и критические изотермы
- •Внутренняя энергия реального газа
- •Фазовые переходы
- •Испарение и кипение
- •Изменение энтропии при фазовых переходах
- •Зависимость температуры фазового перехода от давления. Уравнение Клапейрона — Клаузиуса
- •Явления переноса
- •Общая характеристика явлений переноса
- •Средняя длина свободного пробега
- •Диффузия газов
- •Внутреннее трение в газах
- •Теплопроводность газов
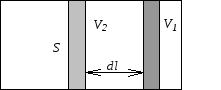
Работа газа
![]()
![]()
![]()
![]()
 Работа газа
Работа газа
Первый закон термодинамики
Существование двух способов передачи энергии термодинамической системе позволяет проанализировать с энергетической точки зрения равновесный процесс перехода системы из какого-либо начального состояния 1 в другое состояние 2. Изменение внутренней энергии системы
U1-2 = U2- U1
в таком процессе равно сумме работы A’1-2 совершаемой над системой внешними силами и теплоты Q1-2 сообщенной системе:
U1-2 = A’1-2 + Q1-2 (2. 3)
Работа A’1-2 численно равна и противоположна по знаку работе A1-2, совершаемой самой системой против внешних сил в том же процессе перехода:
A’1-2 = - A1-2.
Поэтому выражение (2.6) можно переписать иначе:
Q1-2 = U1-2 + A1-2 (2. 3)
Первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение внутренней энергии системы и на совершение системой работы против внешних сил.

Q = dU + A (2. 3)
dU
– внутренняя энергия, является полным
дифференциалом.
![]()
Q и A не являются полными дифференциалами.
![]() Q1-2
=
Q1-2
=
![]() (2.3)
(2.3)
![]() .
.
Исторически установление первого начала термодинамики было связано с неудачами создания вечного двигателя первого рода (перпетуум мобиле), в котором машина совершала бы работу не получая извне тепла и не затрачивая при этом никакого вида энергии. Первый закон термодинамики говорит о невозможности построения такого двигателя.
Q1-2 = U1-2 + A1-2
Применение первого начала термодинамики к изопроцессам.
Изобарный процесс.
р = const

A
=
 = p(V2-V1)
= pV
,
= p(V2-V1)
= pV
,
где р – давление газа, V – изменение его объема.
Т.к.
PV1
=
![]() RT1;
PV2
=
RT1;
PV2
=![]() RT2,
RT2,
то
V2-V1
=
![]()
![]() (T2
– T1)
и
(T2
– T1)
и
А
=
![]() R(T2
– T1);
(2.3)
R(T2
– T1);
(2.3)
Таким образом, получаем, что универсальная газовая постоянная R равна работе, которую совершает моль идеального газа при повышении его температуры на один Кельвин при постоянном давлении.
Учитывая выражение (2.10), уравнение первого начала термодинамики (2.8) можно записать следующим образом
Q = dU + pdV. (2. 3)
Изохорный процесс
V = const, следовательно, dV = 0

А = pV = 0
Q = U.
Q
= U
=
![]()
![]() R
T (2.3)
R
T (2.3)
Изотермический процесс
Т = const,
U = 0 внутренняя энергия идеального газа не изменяется, и
Q = А
A
=
 =
=
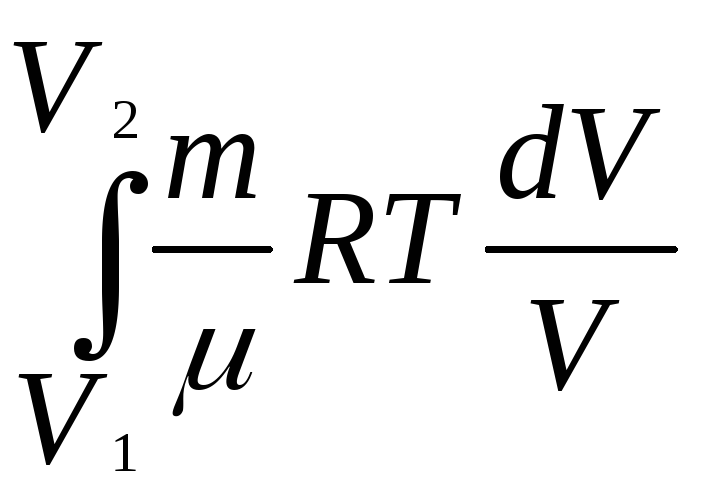 =
=
![]() RTln
RTln![]() (2.3)
(2.3)
Для того, чтобы температура газа при расширении не уменьшалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения, т.е. А = Q.
Практически , чем медленнее протекает процесс, тем с большей точностью его можно считать изотермическим.
Г рафически
работа при изотермическом процессе
численно равна площади заштрихованной
проекции на рис.
рафически
работа при изотермическом процессе
численно равна площади заштрихованной
проекции на рис.
Сравнивая площади фигур под участками изотермы и изобары можно сделать вывод, что расширение газа от объема V1 до объема V2 при одинаковом начальном значении давления газа сопровождается в случае изобарного расширения совершением большей работы.
Теплоемкость газов
Теплоемкостью С какого-либо тела называется отношение бесконечно малого количества теплоты dQ, полученного телом, к соответствующему приращению dT его температуры:
Cтела
=![]() (2.3)
(2.3)
Эта величина измеряется в джоулях на кельвин (Дж/К).
Когда масса тела равна единице, теплоемкость называется удельной. Её обозначают малой буквой с. Она измеряется в джоулях на килограмм.кельвин (Дж/кг.К).Между теплоемкостью моля вещества и удельной теплоемкостью того же вещества существует соотношение
![]() (2.3)
(2.3)
Используя формулы (2.12) и (2.15), можно записать
![]() (2.
3)
(2.
3)
Особое значение имеют теплоемкости при постоянном объеме СV и постоянном давлении Ср. Если объем остается постоянным, то dV = 0 и согласно первому началу термодинамики (2.12) вся теплота идет на приращение внутренней энергии тела
Q = dU (2. 3)
Из этого равенства вытекает, что теплоемкость моля идеального газа при постоянном объеме равна
![]() (2.
3)
(2.
3)
Отсюда dU = CVdT, а внутренняя энергия одного моля идеального газа равна
U = CVT (2. 3)
Внутренняя энергия произвольной массы газа т определяется по формуле
![]() (2.
3)
(2.
3)
Учитывая, что для 1 моля идеального газа
U
=
![]() RT,
RT,
и считая число степеней свободы i неизменным, для молярной теплоемкости при постоянном объеме получаем
Cv
=![]() =
=
![]() (2.3)
(2.3)
Удельная теплоемкость при постоянном объеме
сv
=
![]() =
=![]() (2.3)
(2.3)
Для произвольной массы газа справедливо соотношение:
Q
= dU =
![]()
![]() RdT;
(2.3)
RdT;
(2.3)
Если нагревание газа происходит при постоянном давлении, то газ будет расширяться, совершая над внешними силами положительную работу. Поэтому теплоемкость при постоянном давлении должна быть больше, чем теплоемкость при постоянном объеме.
Если
1 молю газа при изобарном
процессе
сообщается количество теплоты Q
то введя понятие молярной теплоемкости
при постоянном давлении Ср
=![]() можно записать
можно записать
Q = CpdT;
где Cp – молярная теплоемкость при постоянном давлении.
Т.к. в соответствии с первым началом термодинамики
Q
= A
+ dU = RdT +
![]() RdT
=
RdT
=
=(R
+
![]() R)dT
= (R + СV)dT,
R)dT
= (R + СV)dT,
то
Ср
=![]() = R +СV.
(2. 3)
= R +СV.
(2. 3)
Это соотношение называется уравнением Майера:
Выражение для Ср можно также записать в виде:
Ср
= R +
![]() R
=
R
=
![]() .
(2. 3)
.
(2. 3)
Удельную теплоемкость при постоянном давлении сp определим, разделив выражения (2.26) на :
сp
=
![]() (2.3)
(2.3)
При
изобарном сообщении газу массой m
количества теплоты Q
его внутренняя энергия возрастает на
величину U
=
![]() CVT,
а количество теплоты, переданное газу
при изобарном процессе, Q=
CVT,
а количество теплоты, переданное газу
при изобарном процессе, Q=
![]() CpT.
CpT.
Обозначив
отношение теплоемкостей
![]() буквой,
получим
буквой,
получим
 (2.3)
(2.3)
Очевидно, 1 и зависит только от сорта газа (числа степеней свободы).
Из формул (2.22) и (2.26) следует, что молярные теплоемкости определяются лишь числом степеней свободы и не зависят от температуры. Это утверждение справедливо в довольно широком интервале температур лишь для одноатомных газов только с поступательными степенями свободы. У двухатомных газов число степеней свободы, проявляющееся в теплоемкости, зависит от температуры. Молекула двухатомного газа обладает тремя поступательными, степенями свободы: поступательными (3), вращательными (2) и колебательными (2).
Таким
образом, суммарное число степеней
свободы достигает 7 и для молярной
теплоемкости при постоянном объеме мы
должны получить: СV
=
![]() .
.
Из
экспериментальной зависимости молярной
теплоемкости водорода следует, что СV
зависит от температуры: при низкой
температуре (
50 K)
СV
=![]() , при
комнатной СV
=
, при
комнатной СV
=![]() и очень
высокой — СV
=
и очень
высокой — СV
=![]() .
.

Расхождение теории и эксперимента объясняется тем, что при вычислении теплоемкости надо учитывать квантование энергии вращения и колебаний молекул (возможны не любые вращательные и колебательные энергии, а лишь определенный дискретный ряд значений энергий). Если энергия теплового движения недостаточна, например, для возбуждения колебаний, то эти колебания не вносят своего вклада в теплоемкость (соответствующая степень свободы "замораживается" — к ней неприменим закон равномерного распределения энергии). Этим объясняется последовательное (при определенных температурах) возбуждение степеней свободы, поглощающих тепловую энергию, и приведенная на рис. 13 зависимость CV = f(T).
