Rc—цепи

RC—цепи очень широко используются в электронной схемотехнике в качестве времязадающих элементов. Простейшая RC—цепь показана на рис.2.1. Если к ее входным зажимам подсоединить источник постоянного напряжения U_S . (рис.2.1 а), то первоначально незаряженный конденсатор C начнется заряжаться.

При этом напряжение U_C между его обкладками будет экспотенцианально расти, как показано на рис.2.1 в . Одновременно будет экспотенцианально уменьшаться ток I в рассматриваемой цепи (рис.2.1г). Скорость изменения напряжения и тока определяется постоянной времени  = CR. Причем емкость C измеряется в фарадах, сопротивление R—в омах , а постоянная времени  -- в секундах.

Закон изменения напряжения на конденсаторе имеет следующий вид:

U_C ( t ) = U_S (1—e ^{–t / CE}),

где t – время , с.

а) б)

в) г)

Временная зависимость изменения Временная зависимость изменения

I – начальная скорость изменения тока на конденсаторе

напряжения U_S /RC, B/cI – начальная скорость изменения тока

U_S / R²C, A/c

Рис.2.1

В течении начального времени интервала t =  напряжение на конденсаторе возрастет до 0,63 U_S . За следующий такой же временной интервал напряжение изменится на 0,63 (U_S -- 0,63U_S) и т.д.

Теоретически конденсатор никогда не зарядится до максимального напряжения, равного U_S . Однако за время порядка 5 напряжение на нем столь незначительно отличается от U_S , что процесс заряда можно считать закончившимся и принять U_C = U_S .

Заряженный конденсатор запасает энергию в виде электрического поля. Если полностью заряженный конденсатор замкнуть на резистор, он начнет разряжаться и напряжение между его обкладками будет уменьшаться . Скорость уменьшения тока и напряжения, как и в предыдущем случае, определяется постоянной времени  = CR. В этом случае напряжение

u_C (t) = U_Se ^{–t / CR}

в предположении , что начальное напряжение на конденсаторе равно U_S .

Теоретически конденсатор никогда полностью не разрядится, поэтому примерно равно 5 , напряжение и ток оказывается настолько малы, что их можно считать равными нулю.

Передача сигнала прямоугольной формы rc—цепью

На рис.2.2 а. показана сглаживающая RC –цепочка, которая при определенных условиях может выполнять роль интегрирующего звена. На рис.2.2 б приведена RC—цепь, которая в зависимости от своих параметров может выполнять функции разделительного звена, укорачивающей или дифференцирующей цепочки.

Эффективность рассматриваемых цепочек зависит от соотношения между постоянной времени  = RC и периодом входного сигнала t .

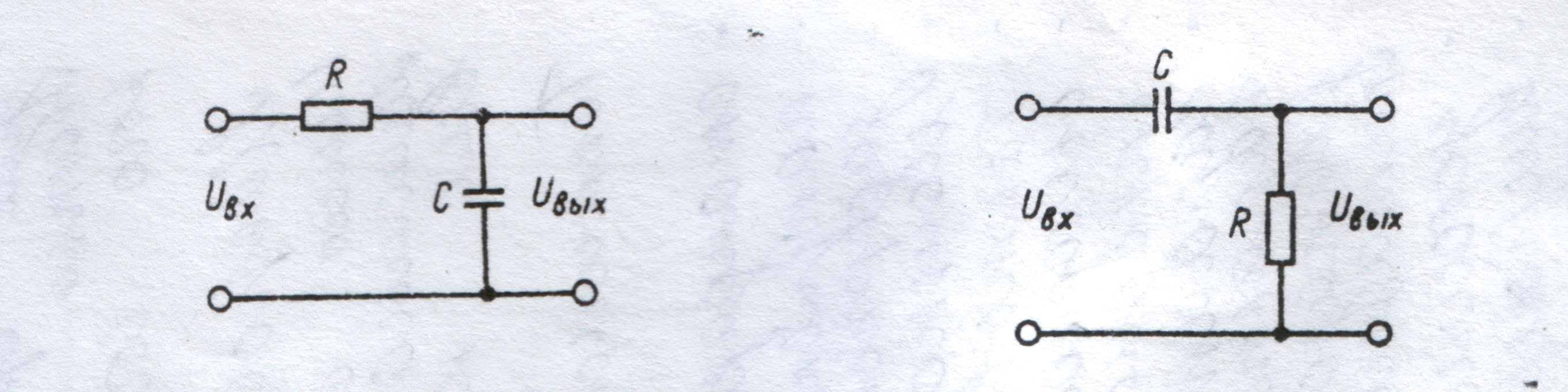
Рис.2.2 ИнтегрирующаяRC—цепь Рис.2.3 ДифференцирующаяRC—цепь

Рис.2.4 Форма импульсов напряжения на рис.2.4

Рис.2.5 Форма импульсов напряжения на рис.2.5

Например, функция интегрирования выполняется тем лучше, чем сильнее выражено неравенство  >> t. При этом автоматически выполняется соотношение U_ВЫХ << U_ВХ.. Функция дифференцирования цепочкой, показанной на рис.2.3, выполняется тем лучше, чем сильнее выражено неравенство  << t. При этом опять—таки U_ВЫХ << U_ВХ. На рисю2.5 нужно обратить внимание на положение нулевой линии на кривых выходного сигнала U_ВЫХ , который является чисто переменной величиной, так как конденсатор C постоянную составляющую напряжения не пропускает.

Пример 2.1 Требуется спроектировать укорачивающую RC—цепь типа данной на рис.2.5 для получения последовательности коротких положительных и отрицательных импульсов. Входным сигналом является последовательность прямоугольных импульсов частотой 1 кГц с временем импульса, равным времени паузы (меандр).

В соответствии с временными диаграммами на рис.2.5 следует выбрать постоянную времени  много меньше входного сигнала, т.е.  << t.

Остановимся на  = RC = 0,1t и некотором среднем значении сопротивлении R, например 10 кОм. В таком случае

C = = = 0,0110^—6 Ф = 10 нФ.

Практически для решения задачи подойдет любое значение C , равное или меньшее 10 нФ. При очень маленькой емкости (скажем, 1 нФ) длительность выходного сигнала будет крайне незначительна, а если фронт нарастания и спада сигнала входного не идеален, то и амплитуда выходного сигнала окажется весьма мала. Поэтому можно остановиться на значении 4,7 или 2,2 нФ.