Пассивные компоненты

Делители напряжения

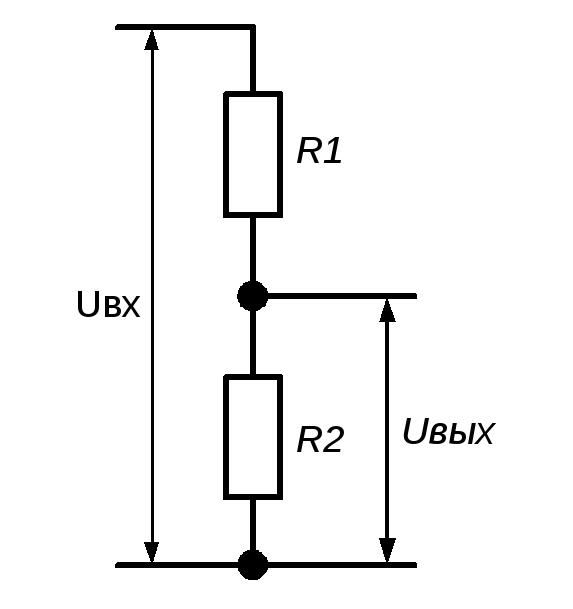
Резисторы часто используются в составе делителя напряжения для получения фиксированного значения напряжения (рис.2.1). В это случае выходное напряжение U_ВЫХ связано с входным U_ВХ (без учета возможного сопротивления нагрузки) следующим соотношением:

U_ВЫХ = U_ВХ

Для получения заданного значения напряжения следует применять высокоточные резисторы. Недостатком простого делителя напряжения является то, что с изменением сопротивления нагрузки выходное напряжение (U_ВЫХ) делителя изменяется. Для уменьшения влияния нагрузки на U_ВЫХ необходимо выбирать сопротивление R2 по крайне мере в 10 раз меньше минимального сопротивления нагрузки. Важно помнить о том , что с уменьшением сопротивлений резисторов R1 и R2 растет ток, потребляемый от источника входного напряжения. Обычно этот ток не должен превышать 1—10 мА.

Пример 1.1. С помощью резистивного делителя нужно получить на нагрузке 100 кОм напряжением 1 В от источника постоянного напряжения 5 В.

Требуемый коэффициент деления напряжения 1/5 = 0,5. Используем делитель, схема которого приведена на рис. 1.1.

Сопротивление резисторов R1 и R2 должны быть значительно меньше 100 кОм. В этом случае при

Рис.1.2 расчете делителя сопротивление нагрузки можно не

учитывать. Следовательно,

R2 = 0,2R1 + 0,2R2 ;

R1 = 4R2 .

Поэтому можно выбрать R2 = 1 кОм, R1 = 4 кОм. Сопротивление R1 получим путем последовательного соединения стандартных резисторов 1,8 и 2,2 кОм из ряда Е 96 с точностью 1% (мощностью 0,125 Вт). Следует помнить , что сам делитель потребляет ток от первичного источника (в данном случае 1 мА) и этот ток будет возрастать с уменьшением сопротивления сопротивлений резисторов делителя.

Законы Киргофа

Законы Киргофа касаются алгебраической суммы токов или напряжений в любой электрической цепи. Когда говорят об «алгебраической» сумме, то имеют в виду , что токи в цепи могут иметь разные направления, а напряжения – разную полярность. Чтобы это учесть, одно из напавлений принимается за положительное, а другое – за отрицательное. Соответсвенно одной группе токов или напряжений присваивается знак (+), а другой – знак минус (--) .

Рис. 1.3. Иллюстрация законов Киргофа.

На рис.1.3, а проиллюстрирован закон для токов в узле : алгебраическая сумма токов в узле равна нулю. При этом считают, что токи, направленные к узлу (I₁, I₄ , I₅), положительные, а токи, направленные от узла, - отрицательные (I₂, I₃).

На рис.1.3, б проиллюстрирован закон для напряжений в контуре : алгебраическая сумма напряжений в контуре равна нулю. При этом выбрано соответствующее направление обхода контура (показано стрелкой). Если при обходе контура батарея пересекается от отрицательного полюса к положительному, то ее ЭДС записывается с положительным знаком (Е₁), если наоборот (--Е₂). В правой части равенства записывается сумма напряжений на резисторах, т.е.

E₁ – E₂ = U₁ + U₂.

Пример 1.1. На рис. 1.4 показана часть схемы питания ЦАП от автономного питания (батареи). Рассчитайте требуемое сопротивление резистора R и полный ток I_S , отбираемой от батареи.

а) б)

Рис.1.4. К примеру 1.1

Сумма токов в узле равна нулю (рис.1.4 а), поэтому

I_S -- I₁ – I₂ – I_Z = 0,

I_S = I₁ + I₂ + I_Z = 50 + 10 + 10 = 70 мА.

В соответствии с выбранным направлением обхода контура (рис.1.4 б) запишем уравнение для напряжений в виде

E – U_Z = U, т.е. U = 9 – 4,7 = 4,3 B.

Через резистор R течет ток I₂ + I_Z = 20 мА, поэтому

R = = = 215 Ом.

Следовательно, можно выбрать ближайший стандартный номинал сопротивления из ряда Е 48 220 Ом 5%.