2.2. Аналитическое выражение первого закона термодинамики

В общем случае, когда в результате подвода теплоты к рабочему телу его температура повышается и вследствие увеличения объема совершается работа, подведенная к телу теплота расходуется на увеличение внутренней энергии тела и на совершение работы. Сказанное может быть выражено уравнением

q = Du +l. (2.13)

Уравнение (2.13) представляет уравнение первого закона термодинамики, записанное в интегральной форме для 1 кг рабочего тела.

Для элементарного процесса уравнение (2.13) принимает вид

dq = du + dl. (2.14)

Если в уравнение (2.14) подставить значение работы по формуле (2.10), то получим

dq = du + pdu. (2.15)

Уравнения (2.13), (2.14) и (2.15) справедливы как для идеальных, так и для реальных газов.

Уравнение (2.15) в применении к идеальным газам, для которых du = c_udT, принимает вид

dq = c_udT + pdu. (2.16)

Для конечного процесса уравнение (2.16) запишется так:

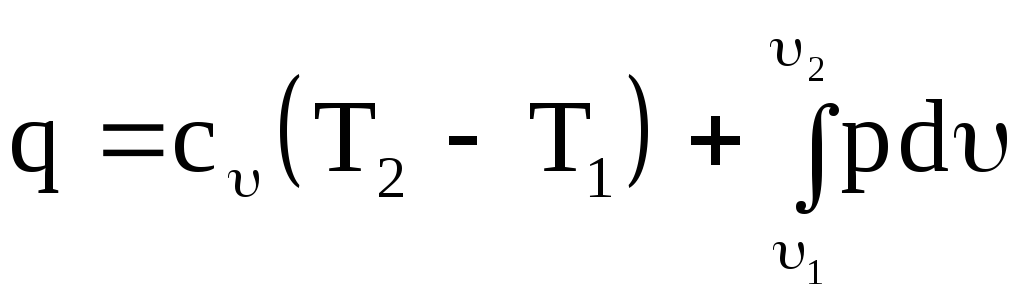. (2.17)

Если в процессе участвует М килограммов газа, то

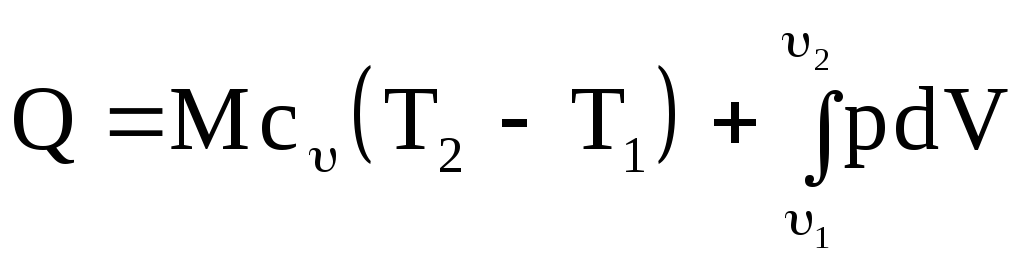. (2.18)

Теплота, изменение внутренней энергии и работа, входящие в уравнение первого закона термодинамики, могут быть положительными и отрицательными, а в отдельных случаях равными нулю.

Принято:

1) теплота подводится к рабочему телу dq >0,

2) теплота отводится от рабочего тела dq < 0,

3) температура рабочего тела растет (dT>0) du>0,

4) температура рабочего тела уменьшается (dT<0) du<0,

5) работа совершается газом при его расширении (du>0) dl>0,

6) работа воспринимается газом в процессах сжатия (du<0) dl<0.

2.3. Энтальпия. Уравнение первого закона термодинамики через изменение энтальпии. Техническая работа

Ранее были рассмотрены четыре параметра состояния рабочего тела p, u, T и u. Для исследования термодинамических процессов и циклов целесообразно ввести новый параметр состояния рабочего тела - энтальпию, который обозначают для 1 кг рабочего тела h,(размерность Дж/кг) и для произвольной массы H, (размерностьДж).

h = u + pu. (2.19)

Таким образом, энтальпия равна внутренней энергии тела, сложенной с величиной pu, представляющей собой работу, которую необходимо затратить, чтобы ввести рассматриваемое тело с объемомVв окружающую среду, имеющую давление p и находящуюся с телом в равновесном состоянии. Эта работа, отдаваемая среде, называется потенциальной энергией давления. Следовательно, энтальпия является суммой внутренней энергии тела и потенциальной энергии давления cреды.

Энтальпию и внутреннюю энергию называют калорическими параметрами.

Введем энтальпию в уравнение первого закона термодинамики. Для этого к правой части уравнения (2.15) добавим и вычтем величину udp:

dq = du + pdu+udp- udp = du + d(pu) -udp = d(u+pu) -udp.

Помня об уравнении (2.19), последнее уравнение перепишем следующим образом:

dq = dh - udp. (2.20)

Выражение (2.20) представляет собой уравнение первого закона термодинамики, записанное через изменение энтальпии.

В интегральной форме уравнение (2.20) запишется как

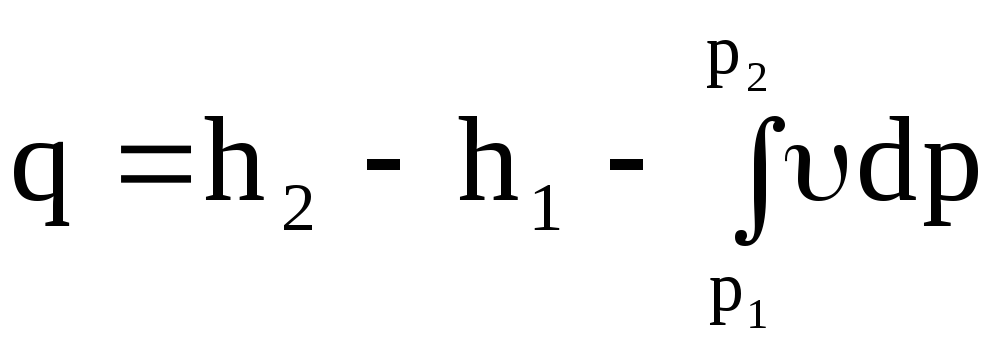. (2.21)

Выведем уравнение для расчета изменения энтальпии. Согласно (2.19) запишем

h = u + pu = u +RT.

Продифференцируем последнее выражение:

dh = du + RdT = c_udT + RdT = (c_u+ R)dT = c_pdT.

Следовательно,

dh = c_pdT (2.22)

или Dh = h₂- h₁= c_p(T₂- T₁). (2.23)

Тогда уравнение (2.20) принимает вид

dq = c_pdT - udp. (2.24)

Из уравнения (2.22) следует, что

(2.25)

Энтальпия, как и внутренняя энергия, является функцией состояния рабочего тела и ее изменение не зависит от характера процесса. Условно считают, что энтальпия и внутренняя энергия равны нулю при t = 0 ^oC.

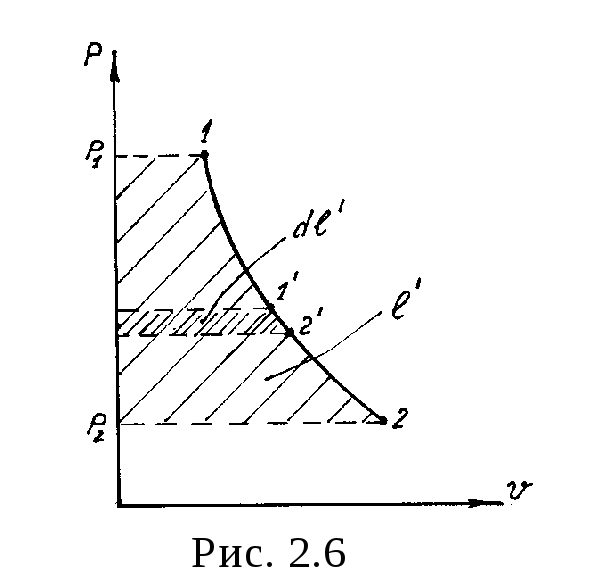
Второе слагаемое в правой части уравнений (2.20) и (2.21) представляет собой техническую (или располагаемую) работу 1 кг рабочего тела. Удельную техническую работу будем обозначать l¢, (размерность Дж/кг).

dl¢= -udp (2.26)

или в интегральной форме

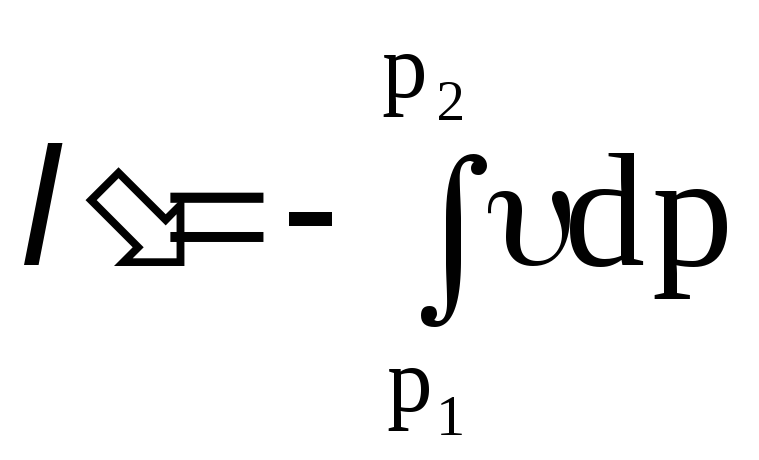. (2.27)

Графически в координатах p и u техническая работа изображается площадью, ограниченной линией процесса, крайними абсциссами линии процесса и осью ординат (рис.2.6). Использование технической работы в ряде расчетов (как мы увидим далее) очень удобно.