6.8. Наложение потенциальных потоков.

Предположим, что имеются два потока с известными потенциалами скорости и , удовлетворяющими уравнению Лапласа. Из теории линейных дифференциальных уравнений, к которым принадлежит и уравнение Лапласа, известно, что сумма частных решений этих уравнений также является их решением. Другими словами, это означает, что потенциал , образованный как , также будет удовлетворять уравнению Лапласа, т.е. будет описывать какой-то новый поток, имеющий потенциал j. Из этого следует, что можно получить новый поток путем сложения (наложения) уже известных. Следует обратить внимание на то, что собственно наложение потоков здесь не производится, а речь идет о сложении потенциалов скорости уже известных течений.

Скорость в каждой точке нового потока является суммой скоростей первоначальных потоков. Задача нахождения нового течения может быть решена как графически, так и аналитически.

Рассмотрим сначала графический метод. Общий подход сводится к следующему. Необходимо построить линии тока течений в одинаковом масштабе, что при достаточной густоте линий тока при пересечении дает фигуру, близкую к параллелограмму (рис. 6.8).

Отрезки AB и AD в каком-то масштабе представляют скорости течения, их результирующая определяется как диагональ параллелограмма (AC). Для построения такой сетки необходимо соблюсти следующее условие: расход между соседними линиями тока обоих течений должен быть одинаков.

Рис. 6.8

В качестве примера рассмотрим картину течения, образующуюся при наложении плоского параллельного потока на сток (рис. 6.9). Как следует из рис. 6.9, частицы жидкости в новом течении будут двигаться по кривым, направленным к стоку.

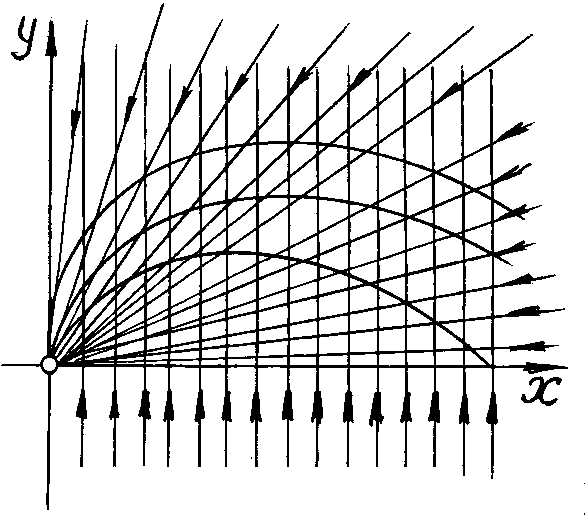
Задача, как отмечалось выше, может быть решена и аналитически. В этом случае должны быть известны j и обоих течений.

Рис. 6.9

Пример 6.4. Выполним сложение источника и стока с одинаковыми расходами, симметрично расположенными относительно начала координат на расстоянии a (см. рис. 6.10).

Потенциалы скорости: источника ; стока - .

Рис. 6.10

Выбираем произвольную точку M с координатами x и y. Потенциал скорости в этой точке , т.е. Выполним некоторые преобразования этого соотношения. Из треугольников MИx и MСx получаем:

Следовательно, потенциал скорости нового течения

(6.29)

Существенно больший интерес представляет функция тока. Как было показано, и .

Аналогично предыдущему

С другой стороны, из рис. 6.10 следует, что , откуда , т.е. . При этом условию (т.е. линии тока) соответствует . Таким образом, линии тока нового течения представляют собой окружности, проходящие через источник и сток.

Рассмотрим теперь картину, образующуюся при сближении источника и стока.

Пример 6.5. Забегая несколько вперед отметим, что получаемое при сближении источника и стока течение называется диполем. В чем особенность рассматриваемой задачи? Если просто предположить, что расстояние , то , и и тождественно равны нулю. Поэтому рассмотрим другой предельный случай. Пусть при расход , но так, что произведение , где M носит название момента диполя. Таким образом,

(6.30)

При этом потенциал скорости диполя

Рассмотрим предел этого отношения

Разберемся теперь в том, что представляет собой выражение, стоящее под знаком предела. Знаменатель можно рассматривать как приращение независимого переменного, а числитель - как соответствующее приращение функции. Действительно, рассмотрим функцию . Придадим x значение и . Если теперь из значения функции, соответствующей , вычесть ее значение при x-a, то получим числитель. Разность значений независимого переменного есть знаменатель. Таким образом, мы должны вычислить предел отношения приращения функции к приращению независимого переменного при стремлении последнего к нулю. Как известно, в математике такой предел называют производной функции, т.е.

Рис. 6.11

Дифференцирование легко выполняется методом подстановок. Пусть ; . Тогда ; ; .

Имеем: ; ,

т.е. .

Таким образом:

(6.31)

Действуя аналогичным образом, можно показать, что

(6.32)

Из чего следует, что линии тока и эквипотенциальные линии - окружности, касающиеся осей Ox и Oy в начале координат (рис. 6.11). Действительно, придавая функции тока постоянные значения, получаем:

где ;

;

;

,

а это и есть уравнения окружностей с разными центрами.