Точность системы автоматического управления Статическая ошибка системы

В системах автоматического управления часто приходится решать задачу стабилизации управляемой величины. Точность поддержания требуемого значения управляемой величины в такой системе можно оценить как разницу между заданным значением управляемой величины и её установившимся значением в системе после окончания переходного процесса:

.

Эта величина получила название статической ошибки системы. При вычислении статической ошибки предполагается, что система находится в статике и все сигналы в ней имеют постоянные величины. Статическая ошибка используется для оценки точности установления в системе заданной постоянной выходной величины после окончания переходного процесса.

Используя передаточную функцию замкнутой системы по ошибке, для изображения ошибки в системе можно записать

, гдепередаточная функция замкнутой системы по ошибке,изображение задающего воздействия.

Для статики, когда все сигналы в системе неизменны, выражение для ошибки можно перенести в область оригиналов

.

Поскольку

, гдеW(p) – передаточная функция разомкнутой системы, то статическую ошибку системы можно вычислить, зная передаточную функцию разомкнутой системы:

, где.

Вместо абсолютного значения статической ошибки часто используют относительную статическую ошибку

.

Если система статическая (т.е. не содержит интегрирующих звеньев), то передаточную функцию разомкнутой системы можно представить в следующем нормированном виде:

, гдеK– коэффициент усиления системы,A^*(p),B^*(p) – нормированные полиномыA(p) иB(p). При этоми. Тогдаи статическая ошибка в статической системе

. Статическая ошибка в статической системе уменьшается с увеличением коэффициента усиления системы. Статическая система всегда будет иметь некоторую ошибку. Физический смысл такой ошибки заключается в необходимости некоторого рассогласования между задающей и выходной величинами системы для получения сигнала управления.

Если в системе управления имеются интегрирующие звенья, то система будет астатической. Для астатической системы первого порядка (содержащей одно интегрирующее звено) передаточная функция разомкнутой системы

и передаточная функция замкнутой системы по ошибке

.

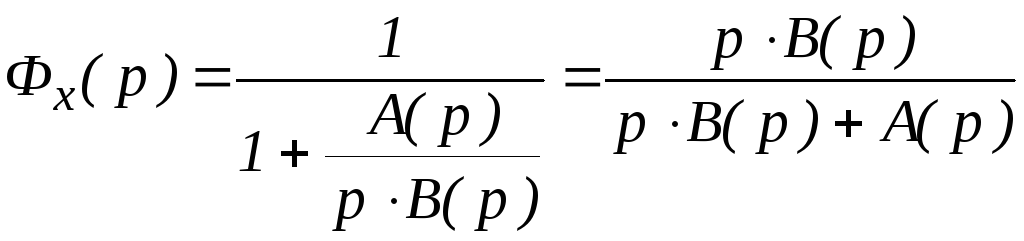В этом случае всегда и, следовательно, статическая ошибка астатической системы будет равна нулю. Таким образом, статическая ошибка в астатической системе в принципе отсутствует, что обуславливает более высокую точность астатических систем, по сравнению со статическими системами. В астатической системе автоматического управления установившееся значение управляемой величины равно заданному значению этой величины.

Вынужденная ошибка системы

Процесс в системе складывается из свободного процесса и вынужденного процесса:

. Для устойчивой системы свободный процесс по истечении времениt_пзатухает и в системе устанавливается вынужденный процесс

Точность поддержания заданного значения управляемой величины в вынужденном режиме характеризуется вынужденной ошибкой системы

.

Вынужденная ошибка хорошо характеризует работу системы автоматического управления в том случае, когда изменения управляющего воздействия происходят существенно медленнее собственных переходных процессов в системе и последними можно пренебречь.

Рассмотрим вычисление вынужденной ошибки системы автоматического управления. Изображение для вынужденной ошибки

.

В общем случае является дробно-рациональной функцией отpи ее можно разложить в ряд Тейлора по степенямрвблизи, тогда

и выражение для вынужденной ошибки системы примет вид

гдепостоянные коэффициенты.

Для полученного изображения вынужденной ошибки на основе свойств преобразования Лапласа легко находится выражение для оригинала ошибки

где ,,…коэффициенты ошибок, полученные выше (C₀– коэффициент статической ошибки,C₁ – коэффициент скоростной ошибки и т. д.).

Коэффициенты ошибки могут быть также получены делением числителя передаточной функции на ее знаменатель. Полученное выражение для вынужденной ошибки позволяет оценить точность системы автоматического управления в установившемся режиме. Вынужденная ошибка, например, хорошо характеризует точность работы следящих систем автоматического управления.