
- •А.В. Федотов теория автоматического управления
- •Список сокращений
- •Основы теории автоматического управления Введение
- •Примеры систем автоматического управления Классический регулятор Уатта для паровой машины
- •Система регулирования скорости вращения двигателей
- •Автоматизированный электропривод
- •Система терморегулирования
- •Следящая система автоматического управления
- •Система автоматического регулирования уровня
- •Обобщённая структура автоматической системы
- •Принципы автоматического управления
- •Математическая модель автоматической системы
- •Пространство состояний системы автоматического управления
- •Классификация систем автоматического управления
- •Структурный метод описания сау
- •Обыкновенные линейные системы автоматического управления Понятие обыкновенной линейной системы
- •Линеаризация дифференциального уравнения системы
- •Форма записи линеаризованных дифференциальных уравнений
- •Преобразование Лапласа
- •Свойства преобразования Лапласа
- •Пример исследования функционального элемента
- •Передаточная функция
- •Типовые воздействия
- •Временные характеристики системы автоматического управления
- •Частотная передаточная функция системы автоматического управления
- •Частотные характеристики системы автоматического управления
- •Типовые звенья
- •5. Дифференцирующее звено.
- •Неустойчивые звенья
- •Соединения структурных звеньев
- •Преобразования структурных схем
- •Передаточная функция замкнутой системы автоматического управления
- •Передаточная функция замкнутой системы по ошибке
- •Построение частотных характеристик системы
- •Устойчивость систем автоматического управления Понятие устойчивости
- •Условия устойчивости системы автоматического управления
- •Теоремы Ляпунова об устойчивости линейной системы
- •Критерии устойчивости системы Общие сведения
- •Критерий устойчивости Гурвица
- •Критерий устойчивости Найквиста
- •Применение критерия к логарифмическим характеристикам
- •Критерий устойчивости Михайлова
- •Построение области устойчивости системы методом d-разбиения
- •Структурная устойчивость систем
- •Качество системы автоматического управления Показатели качества
- •Точность системы автоматического управления Статическая ошибка системы
- •Вынужденная ошибка системы
- •Прямые методы анализа качества системы Аналитическое решение дифференциального уравнения
- •Решение уравнения системы операционными методами
- •Численное решение дифференциального уравнения
- •Моделирование переходной характеристики
- •Косвенные методы анализа качества Оценка качества по распределению корней характеристического полинома системы
- •Интегральные оценки качества процесса
- •Оценка качества по частотным характеристикам Основы метода
- •Оценка качества системы по частотной характеристике
- •Оценка колебательности системы
- •Построение вещественной частотной характеристики
- •Оценка качества сау по логарифмическим характеристикам
- •Синтез системы автоматического управления Постановка задачи синтеза системы
- •Параметрический синтез системы
- •Структурный синтез системы Способы коррекции системы
- •Построение желаемой логарифмической характеристики системы
- •Синтез последовательного корректирующего звена
- •Синтез параллельного корректирующего звена
- •Другие методы синтеза систем автоматического управления
- •Реализация систем автоматического управления Промышленные регуляторы
- •Особенности реализации промышленных регуляторов
- •Настройка промышленных регуляторов
- •Управление по возмущению
- •Комбинированное управление
- •Многосвязные системы регулирования
- •Обеспечение автономности управления
- •Библиографический список
- •Предметный указатель
Структурная устойчивость систем
Если неустойчивую систему можно привести в устойчивое состояние изменением ее параметров, то такая система называется структурно-устойчивой. Если никакое изменение параметров системы не приводит ее в устойчивое состояние, то такая система называетсяструктурно-неустойчивой. Поскольку задача конструктора системы сводится к созданию работоспособной системы (т.е. устойчивой системы), то необходимы способы обеспечения устойчивости структурно-неустойчивых систем.
Р ассмотрим
пример системы, которая задана структурной
схемой, приведенной на рис. 94. Система
состоит из двух инерционных звеньев и
одного интегрирующего звена. Все звенья
соединены последовательно.
ассмотрим
пример системы, которая задана структурной
схемой, приведенной на рис. 94. Система
состоит из двух инерционных звеньев и
одного интегрирующего звена. Все звенья
соединены последовательно.
Исследуем устойчивость этой системы, используя, например, критерий Найквиста. Передаточная функция разомкнутой системы
![]() ,
где
,
где![]() коэффициент усиления
системы.
коэффициент усиления
системы.
Частотную передаточную функцию определим по передаточной функции и представим в виде выражений для модуля и аргумента:
![]() ,
,![]() .
.
АФЧХ системы обладает следующими
особенностями: при
![]()
![]() ,
,![]() ,
а при
,
а при![]()
![]() ,
,![]() .
.
Г рафик
АФЧХ показан на рис. 95. Пунктиром показана
частотная характеристика при большом
коэффициенте усиления системыK.
Замкнутая система в этом случае
неустойчива, поскольку годографW(j)
охватывает контрольную точку(-1,j0).
рафик
АФЧХ показан на рис. 95. Пунктиром показана
частотная характеристика при большом
коэффициенте усиления системыK.
Замкнутая система в этом случае
неустойчива, поскольку годографW(j)
охватывает контрольную точку(-1,j0).
При уменьшении коэффициента усиления системы Kгодограф "стягивается" к началу координат и можно выбрать такое значение коэффициента усиленияK, при котором замкнутая система становится устойчивой (годограф, показанный сплошной линией на рис. 95).
Следовательно, рассматриваемая система является структурно-устойчивой системой. Полуокружность, показанная пунктиром на рис. 95, необходима для условного замыкания АФЧХ астатической системы при использовании критерия устойчивости Найквиста.
Д ругой
пример замкнутой системы показан
структурной схемой на
рис. 96. Эта
система состоит из инерционного звена
и двух интегрирующих звеньев, включенных
последовательно.
ругой
пример замкнутой системы показан
структурной схемой на
рис. 96. Эта
система состоит из инерционного звена
и двух интегрирующих звеньев, включенных
последовательно.
Передаточная функция системы
![]() .
.
Соответственно модуль и аргумент частотной передаточной функции
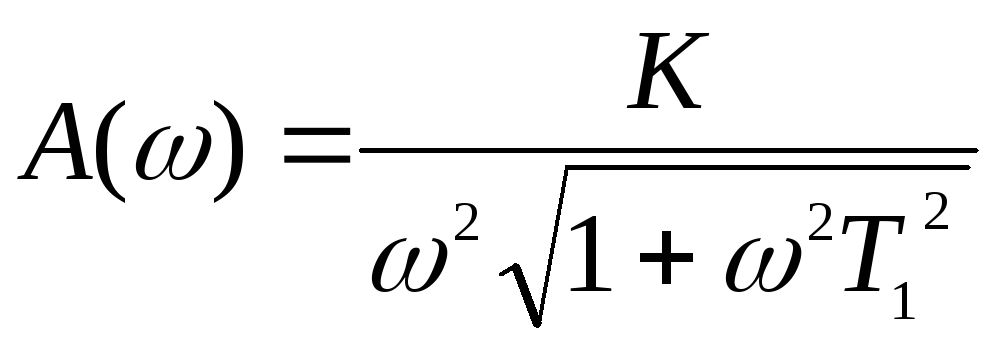
 ,
,![]() .
.
При
![]()
![]() ,
,![]() и при
и при![]()
![]() ,
,![]() .
.
АФЧХ системы показана на рис. 97. Такая система будет неустойчивой при любых значениях K, поскольку контрольная точка(-1,j0) всегда будет находиться внутри контура кривой. Не сможет изменить полученную картину и изменение постоянной времениT1. Рассматриваемая система является структурно-неустойчивой, поскольку привести её к устойчивости изменением параметров системы невозможно.
Сделать структурно-неустойчивую систему устойчивой можно только путём изменения структуры системы. Приведение к устойчивости структурно-неустойчивой системы возможно двумя способами:
введением дополнительных обратных связей, охватывающих неустойчивые звенья.
введением дополнительных звеньев (стабилизирующих звеньев) в структуру системы.
Если в рассматриваемую систему ввести дополнительно реальное дифференцирующее звено с передаточной функцией
![]() ,
,
то передаточная функция системы примет вид
![]() .
.
Новая передаточная функция соответствует структурно-устойчивой системе, как это было видно из предыдущего примера. Дополнительно введённое реальное дифференцирующее звено выполнило функцию стабилизирующего звена.
Сложная система автоматического управления, имеющая в своем составе несколько простых замкнутых систем, является многоконтурной системой. Многоконтурная система будет структурно-устойчивой, если структурно-устойчивы все простые составляющие ее системы.
