Преобразования структурных схем

При рассмотрении структурной схемы системы не всегда в её составе удаётся выделить в чистом виде одно из рассмотренных выше соединений. В этом случае возникает необходимость преобразования структурной схемы к такому виду, чтобы её можно было бы представить типовыми соединениями звеньев. Естественно, что при таком преобразовании сигналы в преобразованной структуре не должны измениться.

Пример структуры, нуждающейся в преобразовании, показан на рис. 64. Из-за перекрещивающихся обратных связей в системе нельзя выделить ни одного типового соединения. Следовательно, для этой структурной схемы нельзя определить общую передаточную функцию.

Преобразование структурных схем сводится либо к переносу точки соединения двух звеньев, либо к переносу внешнего воздействия (сумматора, к которому подводится внешнее воздействие). Для сохранения адекватности преобразованной схемы необходимо выполнять при преобразовании следующие правила.

1. Внешнее воздействие можно перенести с входа звена на его выход, добавив между воздействием и точкой приложения звено с передаточной функцией исходного звена.

Пример показан на рис. 65. Внешнее воздействие f вместе с сумматором переносится со входа звенана выход этого звена. Чтобы сигналы в преобразованной схеме не изменились, при преобразовании добавляется фиктивное звено с передаточной функцией. Слева показана исходная структура, справа – преобразованная.

Для исходной структуры , для преобразованной, т.е. с точки зрения выходного сигнала обе схемы адекватны.

2. Внешнее воздействие можно перенести с выхода звена на его вход, добавив между воздействием и новой точкой его приложения фиктивное звено с передаточной функцией обратной передаточной функции и исходного звена.

На рис. 66 внешнее воздействие fвместе с сумматором переносится с выхода звена(левая структурная схема) на его вход (правая схема). Для обеспечения адекватности преобразованной схемы в её структуру добавлено фиктивное звено с передаточной функцией. Легко убедиться в одинаковости выходной величиныв обеих схемах.

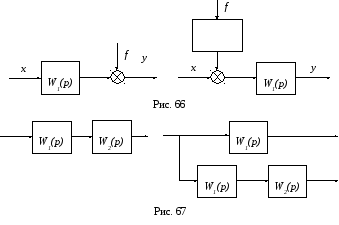
3. Точку присоединения звена 2 можно перенести с выхода звена 1 на его вход, добавив между новой точкой присоединения звена 2 и входом звена фиктивное звено с передаточной функцией .

На рис. 67 звено присоединено к выходу звена(левая схема). Точка присоединения звенапереносится на вход звена(правая схема). Для сохранения сигналов в преобразованную схему добавлено фиктивное звено.

4. Точку присоединения звена 2 можно перенести с входа звена 1 на его выход, добавив между новой точкой присоединения звена 2 и его входом фиктивное звено с передаточной функцией обратной передаточной функции первого звена.

Это правило поясняется рис. 68. В исходной структуре звено присоединено ко входу звена. В преобразованной структуре точка присоединения перенесена на выход звена. Добавление фиктивного звена позволяет сохранить сигналы в системе неизменными.

Передаточная функция замкнутой системы автоматического управления

Всистемах автоматического управления наиболее распространён принцип управления по отклонению. На рис. 69 показана упрощенная принципиальная схема системы автоматического регулирования напряжения генератора постоянного тока, применяемая в системах электропровода.

В этой системе поддерживается заданное значение выходного напряжения генератораГпри всех изменениях нагрузки. Задача управления решается путем сравнения величины выходного напряженияс заданным значением напряжения от опорного источника напряжения. Функциональная схема системы приведена на рис. 70.

В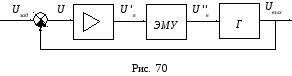ыходной сигналподается на вход системы по цепи отрицательно обратной связи и сравнивается с заданным значением. В результате сравнения определяется ошибка (или рассогласование)

,

сигнал ошибки поступает на вход усилителя и определяет напряжение управления для электромашинного усилителя ЭМУ. В зависимости от напряжения управленияизменяется выходное напряжениеЭМУ, что ведёт к изменению напряжения возбуждения генератораГи соответственно к изменению его входного напряжения. В результате ошибка в системе устраняется, и выходное напряжение генератора всегда будет равно заданному (с погрешностью регулирования, присущей системе).

Электронный усилитель, ЭМУ и генератор опишем передаточными функциями и найдем общую передаточную функциюW(p)этих элементов. Тогда структурную схему системы автоматического регулирования напряжения генератора можно представить в виде, показанном на рис. 71.

Получена структура замкнутой системы, в которой присутствует глобальная единичная обратная связь с выхода системы на её вход. Наличие глобальной обратной связи обеспечивает реализацию управления по ошибке, когда устройство управления постоянно сравнивает фактическое значение выходной управляемой величины с её заданным значением и вырабатывает управляющее воздействие таким образом, чтобы устранить возникающую ошибку.

Свойства замкнутой системы автоматического управления описывает передаточная функция замкнутой системы

. Для структуры на рис. 71 общая передаточная функция может быть найдена с использованием правила нахождения передаточной функции соединения звеньев с обратной связью при единичной обратной связи

, гдеW(p) –передаточная функция разомкнутой системы.

Передаточная функция замкнутой системы иногда называется в литературе главным оператором системы. Передаточная функция замкнутой системы в общем случае является дробной функцией вида

. Поскольку передаточная функцияW(p)разомкнутой системы является дробью:

, то,.

Полином C(p), стоящий в знаменателе выражения передаточной функции замкнутой системы, называетсяхарактеристическим полиномом замкнутой системы. Приравнивание нулю характеристического полинома даётхарактеристическое уравнение замкнутой системы

.

Характеристическое уравнение замкнутой системы является алгебраическим уравнением степени n и имеет в общем случаеn корней. Эти корни являютсяполюсами передаточной функциизамкнутой системы. Решение уравнения, полученного приравниванием нулю полинома, стоящего в числителе передаточной функции,

даетнули передаточной функциизамкнутой системы автоматического управления.

Подстановкой из передаточной функции замкнутой системы можно получить частотную передаточную функцию замкнутой системы

.

В статике передаточная функция разомкнутой системы вырождается в статический коэффициент передачи системы (для статической системы)

,

при этом коэффициент передачи для замкнутой системы