Временные характеристики системы автоматического управления

Временная характеристика представляет собой переходный процесс на выходе системы автоматического управления, возникающий при подаче на вход системы внешнего воздействия. Различают два вида временных характеристик.

Первая временная характеристика получила название переходной характеристикии представляет собой процесс в системе при воздействии на вход системы ступенчатой функции. Изображение Лапласа для переходной характеристики (переходного процесса)

или.

Переходная характеристика является функцией времени и определяется только динамическими свойствами системы:

В обыкновенных линейных системах можно наблюдать три основных вида переходных характеристик (рис. 35).

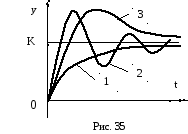
1. Апериодические (монотонные). Первая производная выходной величины не меняет знака.

2. Колебательные периодические. Первая производная выходной величины меняет знак бесконечное число раз.

3. Апериодические колебательные. Первая производная выходной величины меняет свой знак, но отсутствует периодичность смены знака производной и число экстремумов ограничено.

Вид переходной характеристики определяется динамическими свойствами системы или ее элемента. Поэтому при анализе системы автоматического управления обычно стремятся определить её переходную характеристику для оценки свойств системы.

Вторая временная характеристика описывает реакцию (отклик) системы на входное воздействие, описываемое единичной импульсной дельта-функцией. Воздействие дельта-функции выводит систему из состояния равновесия, и дальнейшее поведение системы определяется её собственными свойствами, поскольку внешнее воздействие прекращается ((t) ≡ 0приt > 0). Эта временная характеристика получила названиефункции веса.

Изображение Лапласа единичной импульсной функции X(p) = L{ (t)} = 1, тогда изображение для функции веса

.

Сама весовая функция (функция времени) определится как

.

Весовая функция описывает процесс в системе, возникающий при подаче на вход системы сигнала в виде единичной импульсной функции, и выражается оригиналом передаточной функции системы. Таким образом, вид весовой функции полностью определяется свойствами системы.

Поскольку изображение Лапласа для процесса в системе

,

то сам процесс в системе можно выразить через весовую функцию системы, используя свойство умножения изображений для преобразования Лапласа:

.

Полученная формула позволяет непосредственно описывать переходный процесс в системе при любом входном воздействии по известной функции веса системы. Поскольку весовая функция однозначно определяется передаточной функцией системы, то и характер процесса, описываемого весовой функцией, для обыкновенной линейной системы будет соответствовать переходной характеристике системы. На рис. 36 приведены типовые графики для весовой функции обыкновенной линейной системы автоматического управления. График 1 соответствует апериодическому процессу, график 2 – колебательному, график 3 – колебательному апериодическому.

Частотная передаточная функция системы автоматического управления

Частотные характеристики системы автоматического управления определяются при подаче на вход системы гармонического воздействия

,

где (формула Эйлера).

При подаче такого сигнала на вход и после затухания переходных процессов на выходе установятся также гармонические колебания с той же частотой , но с другой амплитудой и фазой (рис. 37). Тогда для выходного сигнала можно записать

y(t) = y_m=y_m,

где угол фазового сдвига выходного сигнала относительно входного;период сигнала;круговая частота сигнала.

Пусть исследуемая линейная система описывается обыкновенным линейным дифференциальным уравнением

При гармоническом входном сигнале можно в этом уравнении определить все производные входной величины

,

,

....................................................................................

.

Аналогично определятся и производные выходной величины. В результате исходное дифференциальное уравнение можно переписать в виде алгебраического уравнения

Решив это уравнение, получим

Величина W(j)называетсякомплексной частотной функцией (или частотной передаточной функцией). Комплексная частотная функция может быть найдена по передаточной функции путем подстановкиp = j:

Частотная передаточная функция может быть записана в комплексном виде

где А()– модуль частотной передаточной функции; ()– фазовый угол (аргумент);U() = ReW(j)– вещественная составляющая передаточной функции;V() = JmW(j)– мнимая составляющая частотной передаточной функции.

Для частотной передаточной функции справедливы следующие соотношения:

,.

Зависимости А()и()определяют изменение амплитуды и фазы колебаний на выходе системы при изменении частотывходных колебаний. Модуль частотной характеристикиA()определяет коэффициент усиления системы для гармонического сигнала с частотой.