Обыкновенные линейные системы автоматического управления Понятие обыкновенной линейной системы

Система автоматического управления называется обыкновенной линейной, если процесс в системе можно описать обыкновенным линейным дифференциальным уравнением порядка "n". Это уравнение записывается в следующем виде:

где у(t)– выходная (управляемая) величина,х(t)– входное воздействие,c_i, b_j– постоянные коэффициенты уравнения,n > m.

Реальные САУ и их элементы обычно имеют нелинейные статические характеристики и описываются нелинейными дифференциальными уравнениями. Однако на практике в ряде случаев нелинейностью можно пренебречь и описать САУ или ее элемент линеаризованным (приведённым к линейному виду) дифференциальным уравнением.

Таким образом, обыкновенная линейная система является упрощенной математической моделью для описания реальных систем автоматического управления. Процессы в обыкновенной линейной системе описываются обыкновенными линейными дифференциальными уравнениями любого порядка "n". Все сигналы в такой системе непрерывны и связаны между собой линейными функциональными зависимостями.

Обыкновенное линейное дифференциальное уравнение порядка "n" в теории автоматического управления принято записывать в операторном виде

,

где  оператор дифференцирования.

Решение дифференциального уравнения y(t)дает описание процесса в системе, возникающего при воздействии на ее вход сигналаx(t).Решение дифференциального уравнения складывается из общего решения и частного решения:

,

где общее решение дифференциального уравнения без правой части, описывающее свободный процесс в системе независимо от вида входного воздействия;частное решение дифференциального уравнения, зависящее от его правой части и описывающее вынужденный процесс в системе.

Для нахождения общего решения нужно решить уравнение без правой части

.

Общее решение обыкновенного линейного дифференциального уравнения порядка "n" имеет вид

,

где A_i – постоянные интегрирования, определяемые из начальных условий ;p_i – корни характеристического уравнения

.

В статическом состоянии системы все сигналы в ней постоянны и, следовательно, все производные этих сигналов равны нулю. Тогда

и дифференциальное уравнение системы вырождается в статическую характеристику

или ,

где K – коэффициент усиления системы.

Теория обыкновенных линейных систем автоматического управления была разработана в первую очередь и является базой для теории автоматического управления.

Линеаризация дифференциального уравнения системы

В реальных системах автоматического управления практически всегда наблюдаются некоторые нелинейности при преобразовании сигналов. При представлении системы с нелинейностями в виде обыкновенной линейной системы необходимо свести описание процессов в системе к обыкновенному линейному дифференциальному уравнению порядка "n". Процесс получения такого уравнения называется линеаризацией описания системы.

Используются два метода линеаризации описания системы. Первый метод применяется в том случае, когда для системы уже имеется описание процесса в виде нелинейного дифференциального уравнения. Задача состоит в преобразовании этого уравнения к линейному виду. Второй метод применим на стадии получения дифференциального уравнения при описании системы и сводится к пренебрежению нелинейными зависимостями при описании взаимосвязей между сигналами.

Рассмотрим первый метод линеаризации описания системы. Пусть в общем виде некоторая система автоматического управления описывается нелинейным дифференциальным уравнением, которое известно:

.

Процесс в системе начинает рассматриваться с момента приложения ко входу системы внешнего воздействия. Этот момент принимается за нулевой, поэтому время рассмотрения процесса t  0. В общем случае в начальный момент времени все сигналы в системе отличны от нуля и совокупность этих сигналов описывает начальное состояние системы (нулевые условия):

.

Поскольку нас интересует поведение системы при t0, то исходное состояние системы может быть принято за нулевое и в дальнейшем мы можем учитывать только отклонения сигналов в системе от начальных значений. В этом случае говорят, что уравнение системы записывается в отклонениях.

Линеаризация исходного нелинейного дифференциального уравнения заключается в разложении нелинейной функции в степенной ряд Тейлора и в отбрасывании членов ряда Тейлора, порождающих нелинейную зависимость. Обозначим

,,

тогда

.

При линеаризации все члены ряда Тейлора высшего порядка малости отбрасываются и принимается

где ,

.

В результате получаем линеаризованное дифференциальное уравнение системы "в отклонениях" (или "в вариациях")

где коэффициенты дифференциального уравнения.

При этом исходное дифференциальное уравнение можно переписать в виде

Рассмотрим графическую интерпретацию проведенной линеаризации (рис. 27). На рис. 27а криваяBсоответствует нелинейной зависимостиy(x). Если нелинейную функциюy(x)разложить в ряд Тейлора в точкеO(x₀,y₀) и отбросить нелинейные члены ряда, то криваяB будет заменена касательнойC, а зависимостьy(x)преобразуется к виду, гдепри.

Если точку O(x₀,y₀) принять за начало координат, то получим зависимость между приращениямиΔyиΔx(рис. 27б)

, где.

В результате линеаризации исходное нелинейное дифференциальное уравнение

при начальных условиях можно представить в виде линеаризованного уравнения

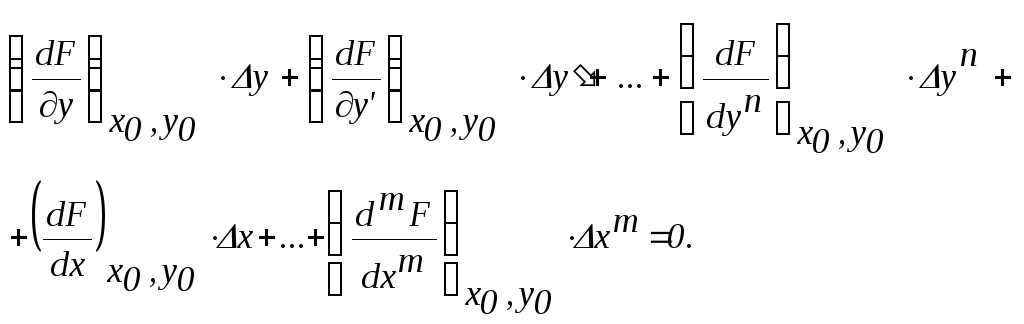
Поскольку значения производных, вычисленные при постоянных x₀, y₀, дают числовые величины, то линеаризованное уравнение можно записать в отклонениях как

где yиx– отклонения этих величин от значенийx₀иy₀.

Пример. Рассмотрим нелинейное дифференциальное уравнение второго порядка

, или.

Выделим нелинейную функцию

.

Пусть начальные условия , тогда

^,,

После замены нелинейной функции первыми членами ряда Тейлора получим новое приближённое уравнение

.

Поскольку вновь полученное уравнение по-прежнему нелинейно, вторично подвергаем его линеаризации

Окончательный вид линеаризованного уравнения:

В новом уравнении , оно записано для отклонений. Это уравнение линейно.

Второй метод линеаризации заключается в том, что реальные нелинейные зависимости между сигналами уже при составлении уравнений аппроксимируются линейными зависимостями вида

и уравнение системы изначально составляется в отклонениях:

При рассмотрении обыкновенных линейных систем автоматического управления в дальнейшем рассматриваются линеаризованные дифференциальные уравнения, записанные в отклонениях. При этом везде будет подразумеваться

Пределы, в которых справедлива замена нелинейных дифференциальных уравнений линеаризованными, определяются допустимой величиной отклонения реальных характеристик от линеаризованных и возникающей при анализе погрешности расчета системы. Вопрос о допустимости линеаризации решается в каждом конкретном случае. Существуют случаи, когда линеаризация недопустима из-за существенного искажения реальных процессов.