
методичка по инженерной графике / Lektsia_6-s1
.pdf
Лекция 6 |
(Задачи 10, 11, 12, 13) |
Изображение прямой на комплексном чертеже
Прямая в пространстве может быть задана двумя способами 1.С помощью задания одной точки и направления
l2 |
2. С помощью задания двух точек |
A2 |
B2 |
x1,2 |
A2 |
|
x1,2 |
A1 |
l1 |
|
A1 B1
Классификация прямых
1. Прямые общего положения. Если прямая линия не параллельна и не перпендикулярна не к одной из основных плоскостей проекций, то эту прямую называют прямой общего положения.
|
B2 |
N2 |
B2 |
|
|
|
|
|
A2 |
A2 |
|
M2 |
|
|
x1,2 |
x1,2 |
|
B1 |
B1 |
N1 |
A1 |
|
|
A1 |
M1 |
|
|
|
Точка M – задает горизонтальный след прямой.
Точка N – задает фронтальный след прямой.
1
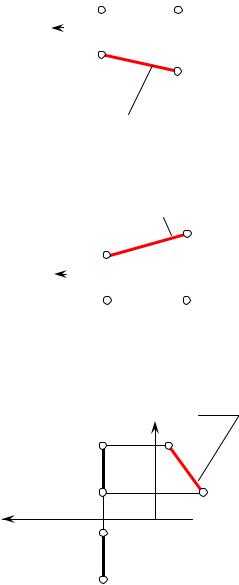
2. Прямые уровня. Если прямая параллельна какой либо из основных плоскостей проекций, то такую прямую называют прямой уровня.
a)Если прямая параллельна горизонтальной плоскости проекции, то ее называют горизонталью (или горизонтальной уровня);
|
|
A2 h2 |
B2 |
|||||
x1,2 |
|
|
|
|
|
A2B2 // x1,2 |
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
A1B1 – натуральная величина отрезка (Н.В.) |
|
|
|
|
h1 |
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
A1 |
|
B1 |
|||||
|
|
|||||||
|
|
Н.В. |
||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
б) Если прямая линия параллельна фронтальной плоскости проекций, то ее называют фронталью (или фронтальная уровня);
Н.В.
|
A2 f2 |
|
|
B2 |
A1B1 // x1,2 |
||
|
|
|
|||||
x1,2 |
|
|
|
|
|
A2B2 – натуральная величина отрезка. |
|
|
|
|
|
||||
|
|
|
|
f1 |
|
|
|
|
|
|
|
|
|
B1 |
|
|
A1 |
|
|
||||
в) Если прямая параллельна профильной плоскости проекции, то ее называют
профильной уровня; |
Н.В. |
|
|
A2 |
A3 |
B2 |
B3 |
x1,2 |
|
A1 |
|
B1 |
|
A2B2 ┴ x1,2
A1B1 ┴ x1,2
A3B3 - натуральная величина отрезка.
3. Проецирующие прямые – это прямые перпендикулярные плоскостям проекций.
Отрезок АВ является – горизонтально проецирующим, т.е. перпендикулярным горизонтальной плоскости проекции П1.
2
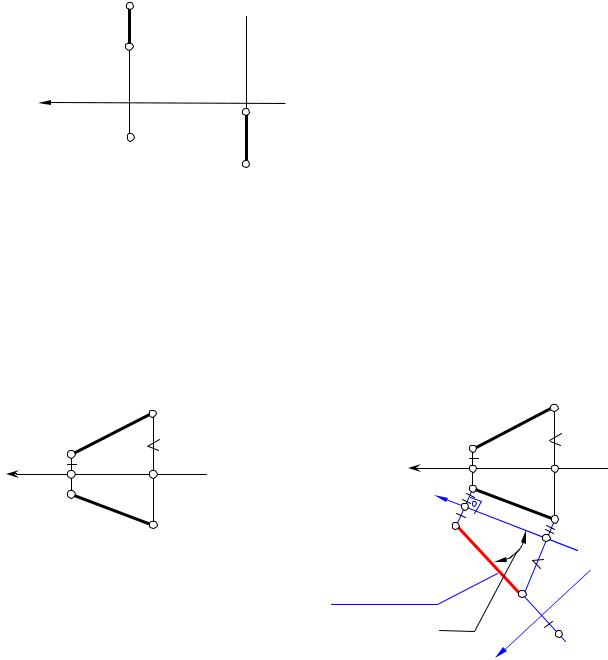
B2
A2
x1,2
A1=B1
 C2=D2
C2=D2
C1
D1
Отрезок СD является – фронтально проецирующим, т. е. перпендикулярным фронтальной плоскости проекции. Точки A1 и B1 – называют горизонтально конкурирующими точками.
Определение натуральной величины отрезка прямой Проецирование отрезка в точку
Отрезок прямой общего положения в общем случае проецируется на основные плоскости проекций с искажением, для определения натуральной величины отрезка прямой необходимо использовать дополнительную плоскость проекций параллельную отрезку AB.
|
|
B2 |
x1,2 |
A2 |
|
Ax |
Bx |
|
|
A1 |
|
B1
|
|
B2 |
x1,2 |
A2 |
Bx |
Ax |
||
|
|
|
|
A1 |
|
x1,4 |
|
|
Ax/ |
B1 |
|
A4 |
Bx/ |
|
Натуральная величина |
||
|
Н.В.
αB4  Bx//=Ax//
Bx//=Ax//
x4,5 A5=B5
Алгоритм решения
1. x1,4 // A1B1. Строим ось x1,4 // A1B1,задающую дополнительную плоскость
П4;
2. Ax/A1 ┴ x1,4, Bx/B1┴ x1,4. Проводим линии проекционной связи через точки
A1, B1 перпендикулярные оси x1,4;
3. AxA2=Ax/A4 BxB2=Bx/B4. Откладываем отрезки AxA2=Ax/A4 BxB2=Bx/B4;
3
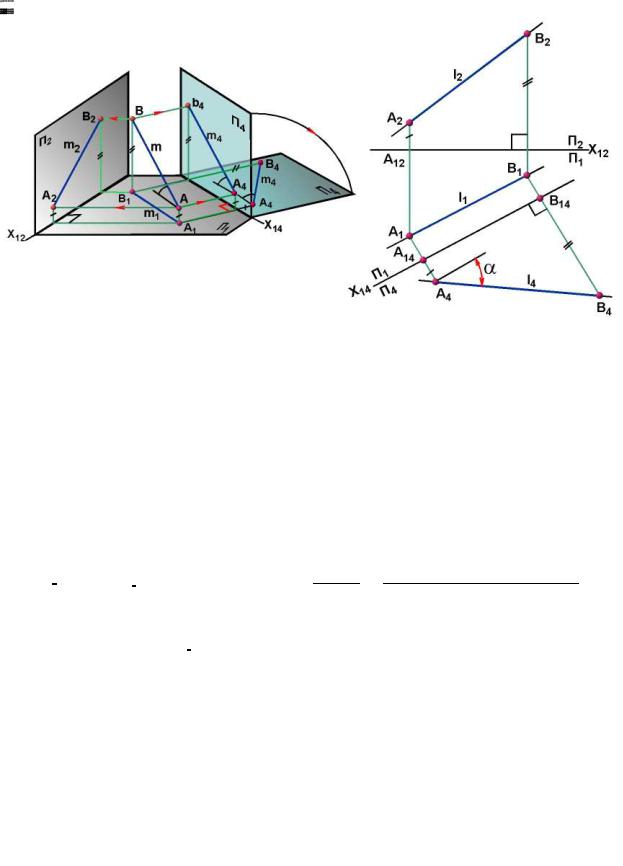
4. A4B4 – Н.В. Отрезок A4B4 определяет натуральную величину отрезка прямой АВ. Угол α определяет угол наклона к горизонтальной плоскости проекций.
Проецирование отрезка прямой в точку
Для проецирования отрезка в точку необходимо использовать еще одну дополнительную плоскость проекций П5. При этом в пространстве отрезок должен быть перпендикулярен данной плоскости П5.
Алгоритм решения
1. Определяем натуральную величину отрезка прямой описанным выше методом;
2. x4,5 ┴ A4B4 Строим ось x4,5 ┴ A4B4, где A4B4 – натуральная величина отрезка прямой, ось x4,5 задает дополнительную плоскость проекций П5.
3.Определяем проекции точек на линии проекционной связи перпендикулярной оси x4,5 используя правило: откладываем расстояние от
старой проекции до старой оси.
Определение натуральной величины отрезка с использованием метода прямоугольного треугольника
На рисунке видно, что натуральная величина отрезка BC прямой общего положения является гипотенузой прямоугольного треугольника BC–1 . В этом
треугольнике один катет B–1 параллелен плоскости H |
и равен до длине |
|
горизонтальной проекции отрезка BC ([B–1 ] |
[B0C0]), |
а величина второго |
4
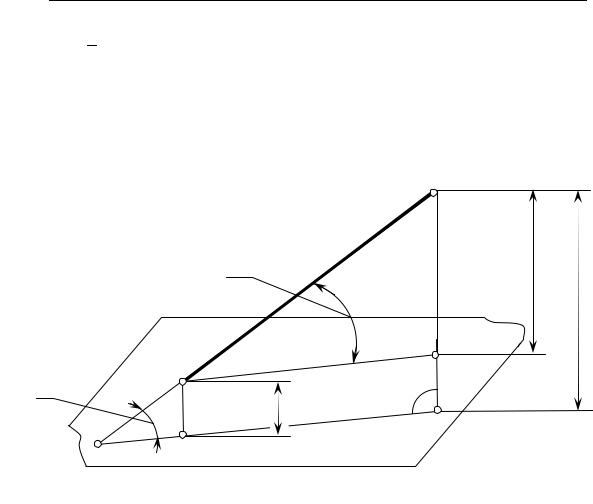
катета равна разности расстояний точек C и B до плоскости проекций П1 (|C–1 |
= Zc − Zb = ∆z).
Для определения натуральной величины отрезка BC прямой общего положения необходимо:
1.В качестве одного катета принимаем горизонтальную проекцию B1C1.
2.Длину другого катета |C0C1| = |C212| = ∆z откладываем на прямой C0C1
C212 .
3.Длина гипотенузы B1C0 равна длине отрезка BC .
Другое построение выполнено на фронтальной проекции. Проекция B2C2
отрезка взята за один катет прямоугольного треугольника. Длина другого катета равна разности расстояний от концов отрезка до плоскости П2 (|B1B2| = yb – y c = ∆y). Длина гипотенузы B0B2 равна длине отрезка BC.
α
|
П1 |
|
α |
B |
|
Zb |
||
|
||
|
M |
|
|
B0 |
C
Zb |
|
Zc – |
Zc |
1
. |
C0
5

|
|
β |
C2 |
|
|
|
|
B0 |
|
∆z |
|
|
|
||
∆y |
B2 |
|
12 |
x1,2 |
|
||
|
|
|
|
∆y |
|
|
C1=11 |
|
|
∆z |
|
|
α |
|
|
|
B1 |
|
|
|
|
|
C0 |
Угол между прямой и плоскостью проекций определяется как угол между прямой и её проекцией на эту плоскость. На рисунке таким углом
между прямой BC и плоскостью H является угол α ( С1 B1 С0). Угол β наклона прямой к фронтальной плоскости проекций определяется из треугольника B2B0С2, построенного на фронтальной проекции.
С1 B1 С0). Угол β наклона прямой к фронтальной плоскости проекций определяется из треугольника B2B0С2, построенного на фронтальной проекции.
Принадлежность точки прямой
Теорема №1 Если точка принадлежит прямой, то одноименные проекции точки принадлежат одноименным проекциям прямой.
|
|
|
C2 |
С2 |
l2 |
C l |
D2 |
l2 |
D l |
|
l2 |
C1 l1 |
D1 l1 |
||||||
|
|
|
|||||||
x1,2 |
|
D2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
l1
D1  C1
C1
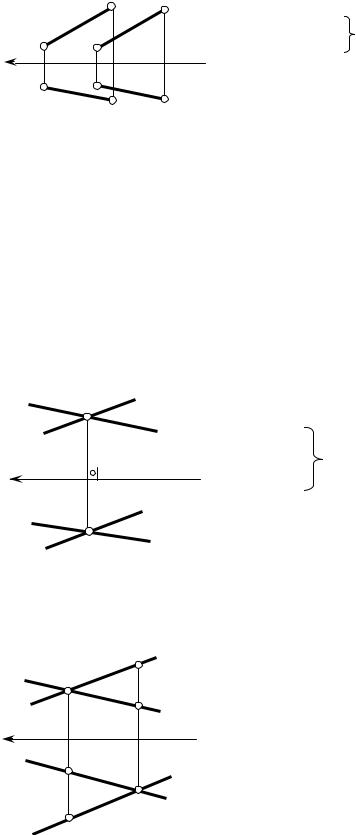
Взаимное положение прямых
1.Параллельные прямые Теорема №2 Если прямые в пространстве параллельны, то их одноименные
проекции также параллельны.
6
|
B2 |
D2 |
|
|
|
A2 |
|
A2B2 |
// C2D2 |
AB // CD |
|
|
|
||||
x1,2 |
C2 |
|
A1B1 // C1D1 |
||
|
|
||||
A1 |
C1 |
|
|
|
|
|
D1 |
|
|
|
|
|
|
B1 |
|
|
|
2.Прямые пересекаются
Теорема №3 Если прямые в пространстве пересекаются, то их одноименные проекции так же пересекаются, при этом проекции точек пересечения принадлежат одной линии проекционной связи.
|
|
|
m2 |
|
K2 |
||
|
|
|
l2 |
|
|
|
m2 Ç l2=K2 |
x1,2 |
|
|
m1 Ç l1=K1 m Ç l=K |
|
|
||
K1K2 ┴ x1,2
m1
K1
l1
3.Скрещивающиеся прямые
Это прямые, которые не параллельны между собой и не пересекаются.
m2 |
N2=M2 |
L2 |
l2 |
|
F2 |
|
|
|
x1,2 |
|
|
m1 |
|
|
|
M1 |
|
l1 |
N1 |
F1=L1 |
|
|
Точки N, M – является фронтально конкурирующими.
Точки F,L – является горизонтально конкурирующими.
7
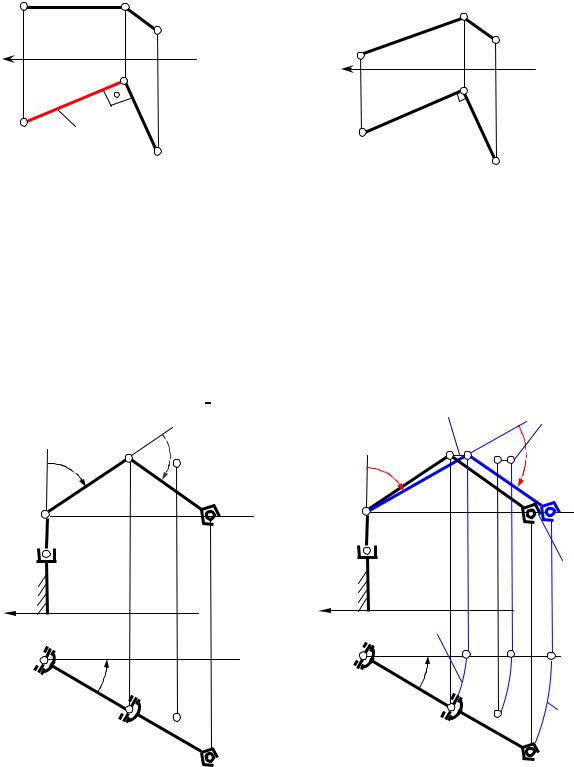
Теорема о проецировании прямого угла |
|
|
|
|
|
|||
Теорема №4 Прямой угол проецируется в прямой, если одна из его |
|
|||||||
сторон проецируется в натуральную величину. В общем случае прямой угол |
|
|||||||
проецируется с искажением. |
|
|
|
|
|
|
||
A2 |
B2 |
|
|
B2 |
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
x1,2 |
|
A2 |
|
|
C2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
x1,2 |
|
|
|
|
|
|
|
B1 |
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
||
Н.В. |
C1 |
|
|
|
|
|
|
|
A1 |
|
A1 |
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Угол Ð АВС прямой |
Угол Ð АВС не прямой |
|
|
|||||
Определение натуральных величин отрезков прямых с помощью |
|
|||||||
|
|
вращательных движений |
|
|
|
|
|
|
|
|
Задача №1. |
|
|
|
|
|
|
Определить натуральные величины длин звеньев механизма, на |
|
|||||||
комплексном чертеже. Определить минимальное удаление звеньев от |
|
|||||||
препятствия, заданного точкой Е при изменении угла j1. |
|
|
|
|
|
|||
|
|
|
с2 |
C2 / |
|
|
E/2 |
|
/ |
C2 |
φ3/ |
C2 |
|
E2 |
|
||
φ2 |
|
E2 |
φ2 |
|
|
|
φ3 |
|
l2 |
|
l2 |
|
|
|
D2 |
/ |
|
|
|
|
|
|
||||
|
|
|
B2 |
|
|
|
||
B2 |
|
D2 |
|
|
D2 |
|
|
|
A2 |
|
A2 |
|
|
|
|
||
|
|
|
|
|
d2 |
|
||
|
|
|
|
|
|
|
|
|
x 1,2 |
|
|
x 1,2 |
|
|
|
|
|
l1=B1=A1 |
|
|
c1 |
|
|
|
D1 / |
|
|
|
l1=B1=A1 |
|
|
|
|||
|
φ1 |
|
φ1 |
C1 |
/ |
E1 |
/ |
|
|
C1 |
E1 |
C1 |
|
|
E1 |
d1 |
|
|
|
|
|
|
||||
|
|
D1 |
|
|
|
|
D1 |
|
|
|
|
8 |
|
|
|
|
|
План решения:
1.Вращаем плоскость Σ, содержащую звенья BC и CD вокруг фронтально-
проецирующей прямой l(l1,l2) (изменением значения обобщённой координаты φ1) до нового положения точек A1, C1 /, D1 /.
2.Изображаем положения траекторий движения c2 и d2 точек C и D на фронтальной проекции. По проекционной связи находим точки C2 / и D2 /.
3. Отрезки B2 C2 / и C2 / D2 / – определяют н.в. длин звеньев механизма, а углы φ2 и φ3 – значения обобщённых координат.
9
