2. Вычисление длины дуги различных кривых

а) Вычисление длины дуги в прямоугольных координатах

А В 0 а в х Рисунок 13

1) Если линия задана уравнением, то длина ее дуги АВ вычисляется по формуле : .

Рассмотрим пример:

Вычислить длину дуги кривой, заданной уравнением от начала координат до точки.

Решение. Найдем производную функции , т. е.

;

т.к. О(0; 0), в нашем случае

2) Если уравнение кривой задано в параметрическом виде, т. е. 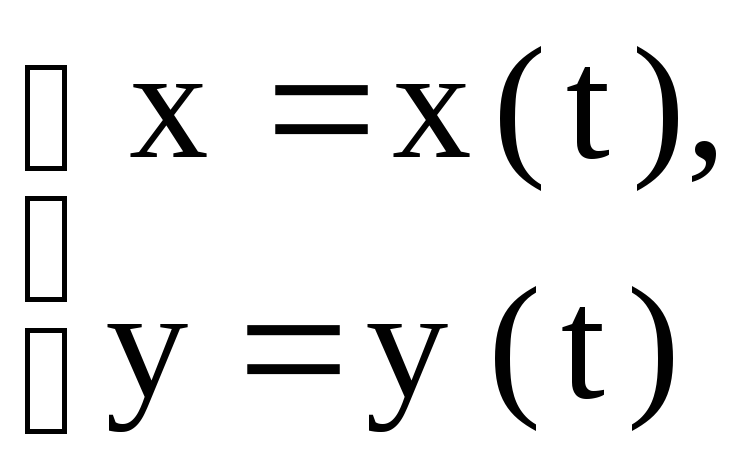, то длина дуги вычисляется по формуле:

.

где - значения параметра, соответствующие концам дуги.

Рассмотрим пример.

Найти длину дуги полукубической параболы, заданной параметрически между точками А ( 1; 1 )и В ( 4; 8 ) (см. рис. 10).

Решение. Так как , в нашем случае, найдем значения параметра, соответствующие концам дуги.

Для этого абсциссы точек А и В подставляем в уравнение , тогда при нахождениинужно решить.

Так как точки расположены на кривой над осью ,.

Аналогично получим уравнение , по тем же соображениям выбираем значение.

Тогда

(введем новую переменную находим пределы интегрирования для:).

Ответ: .

б) Вычисление длины дуги в полярных координатах

Если кривая АВ задана уравнением в полярных координатах , где, то.

Рассмотрим пример.

Вычислить дугу кардиоиды, заданной в полярной системе координат: , где(т.е. той части кривой, которая расположена выше оси).

Решение.

Рассмотрим уже известную нам кривую (см. рис. 12). Применим формулу

, где , тогда

Задания для самостоятельной работы. Приложения определенного интеграла

I. Вычислить площадь фигур, ограниченных линиями:

Ответы:

1.
2.и координатными осями.
3.и осью Оу.
4. - эллипс.
5. Одним витком спирали Архимеда .
6. - лемниската Бернулли.
7. и.
II. Найти длины дуг следующих кривых:
1. от до .	.
2. .	.
3. ,.	.
4. от до.	.

3. Объем тела вращения

1) Если тело образовано вращением плоской фигуры вокруг оси Ох, то его объем равен

0 а в х Рисунок 14

2) Если же тело образовано вращением плоской фигуры вокруг оси Оу, то его объем равен

у 0 x Рисунок 15

.

Рассмотрим пример:

Найти объемы тел, образованных вращением фигуры, ограниченной линиями: ;;.

а) вокруг оси Ох; б) вокруг оси Оу;

Решение.

а) Изобразим тело, получающееся в результате вращения данной плоской фигуры вокруг Ох:

у 4 0 1х - 4	Ответ: куб.ед.
у В 4 С х - 4 0 F 4	б) Изобразим тело, получающееся в результате вращения фигуры вокруг оси Оу

При вращении данной плоской фигуры вокруг оси Оу образуется тело с «вырезанным» круговым цилиндром, получающимся при вращении прямоугольника ОВСF вокруг Оу, причем он состоит из двух цилиндров с объемами . Найдемобъем тела, полученного при вращении криволинейной трапеции АВСD вокруг Оу:

4 В С А К Д 0 F Е х

Тогда (куб. ед.).

Ответ: куб. ед.