Алгоритм симплекс-метода

Шаг 1. Объявить начальную симплексную таблицу и соответствующий опорный план текущими.

Шаг 2 (Проверка оптимальности). Просмотреть строку F текущей таблицы (кроме свободного члена).

а) Если в строке F нет отрицательных элементов (все , то текущий опорный план – оптимальный; если при этом нет и нулевых элементов, то оптимальный план - единственный, если нулевые элементы есть, то множество оптимальных планов бесконечно.

б) Если в строке F есть отрицательные элементы, выбрать среди них наибольш ий по модулю и объявить соответствующий столбец разрешающим.

Шаг 3 (Выбор разрешающего элемента). Просмотреть разрешающий столбец текущей таблицы (кроме элемента строки F).

а) Если в разрешающем столбце нет положительных элементов (все , то целевая функция не ограничена и оптимальных планов нет.

б) Если в разрешающем столбце есть положительные элементы, то для всех содержащих эти элементы строк вычислить и записать в столбец отношения свободных членов таблицы к соответствующим элементам разрешающего столбца -симплексные отношения (в строках, содержащих нулевые или отрицательные элементы разрешающего столбца, если такие имеются, вместо симплексных отношений поставить прочерки). Строку с минимальным симплексным отношением объявить разрешающей, элемент на пересечении разрешающей строки с разрешающим столбцом объявить разрешающим.

Шаг 4 (Улучшение плана). Выполнить симплексное преобразование текущей таблицы с разрешающим элементом, выбранным на шаге 3б); объявить полученную таблицу и соответствующий опорный план текущими.

Шаг 5. Перейти к шагу 2.

Результатом применении симплекс-метода будет цепочка допустимых симплексных таблиц и соответствующих опорных плановтакая, чтоВ большинстве задач ЛП значения целевой функции строго возрастают и решение задачи завершается через конечное число шагов на таблице, удовлетворяющей требованиям шага 2а) или шага 3а). Особые случаи всегда связаны с вырожденностью решаемой задачи. Задача ЛП называется вырожденной, если у нее есть опорные планы, в которых кроме всех свободных переменных равны нулю и некоторые базисные. Разберем подробно простейший из таких особых случаев.

Пример 10. Решить симплекс-методом задачу ЛП с ограничениями

Решение. Начальная таблица находится так же, как в предыдущих примерах. Одна из возможных цепочек состоит из трех таблиц:

Начальной таблице соответствует опорный план

В строке F таблицы есть отрицательные элементы, (-3) – наибольший из них по модулю, поэтому столбецразрешающий (выделен). В разрешающем столбцеесть положительные элементы (в данном случае все). Вычисляем симплексные отношения 12/4,8/4,8/4 (столбец ). Здесь оказалисьдве строки с минимальным симплексным отношением, выбираем в качестве разрешающей одну из них, например(выделена). Элемент 4 на пересечении строкии столбцаразрешающий. Далее выполняем симплексное преобразование таблицыпо правилам 1) - 5) и переходим кменяем местамизаменяем разрешающий элемент 4 на 1/4; остальные элементы разрешающей строки, 1 и 8, делим на 4; остальные элементы разрешающего столбца, 4, 4 и (-3), делим на (-4); все оставшиеся элементы, не принадлежащие ни строкени столбцупересчитываем по правилу четырехугольника. Например, -2 в строкеF заменяем на 3 в столбце– наТеперь таблицаи опорный плантекущие,и все операции начиная с шага 2 повторяются с таблицейВ строкеF таблицы еще есть отрицательный элементв разрешающем столбцеесть положительные элементы 2 и 1/4. После вычисления симплексных отношений ( почему в строкевместо отношения стоит прочерк?) и выбора разрешающего элемента 2 надо выполнить симплексное преобразование таблицы

т. е. перейти к При этом целесообразно начать вычисления с элементов строкиF: если они окажутся неотрицательными (в данном случае так и будет: получатся ), тобудетзаключительной, ей соответствует оптимальный опорный план. Чтобы выписать этот план и , нужен только столбец свободных членов таблицы, «внутренние» элементыможно не вычислять. Итак, в данной задачеединственный оптимальный план и

При втором варианте выбора разрешающей строки в вместополучается другая цепочка таблиц:где

Здесь и в дальнейшем столбцы симплексных отношений опущены и сразу выделены разрешающие элементы. Вторая цепочка тоже приводит к оптимальному плану (конечно, тому же самому ведь он единственный!). Заметим, что в каждом из опорных плановтаблицесть базисное переменное с нулевым значением (см. столбцы свободных членов) - задача вырождена. Более того, хотя таблицы различные.

Пример 10 показывает, что при применении симплекс-метода к вырожденной задаче нескольким последовательным таблицам может соответствовать один и тот же опорный план (во второй цепочке). Оказывается, что в других (более сложных) вырожденных задачах возможна следующая ситуация: нескольким таблицам соответствует один и тот же опорный план и на некотором шаге очередная из этих таблиц повторяет одну из предыдущих – происходитзацикливание. В теории ЛП разработаны различные варианты уточнения основного алгоритма симплекс-метода, позволяющие избежать зацикливания, но при решении практических задач они применяются очень редко, так как их использование сильно замедляет вычислительный процесс, а вероятность зацикливания ничтожно мала.

В заключение приведем пример решения задачи о ресурсах с помощью симплекс-метода.

Пример 11. В таблице 4 представлены исходные данные задачи о ресурсах:

запасы ресурсов (последний столбец), доходы от реализации одной единицы каждого вида продукции (последняя строка), технологическая матрица (остальная часть таблицы). Построить математическую модель задачи. Найти оптимальный план производства, максимальный доход и остатки ресурсов.

Таблица 4

Решение. Обозначим планируемые объемы производства по видам продукции. Математической моделью будет задача ЛП в стандартной (записана слева) или канонической (справа) форме:

,

Смысл переменных - остатки ресурсов. В стандартной форме - три переменные, графическое решение практически невозможно (попробуйте). Решим задачу симплекс-методом. Начальная таблицаздесь (как и в любой задаче о ресурсах) находится просто: за базисные надо выбрать переменные. Далее цепочка таблиц определяется шагами симплекс-метода однозначно.

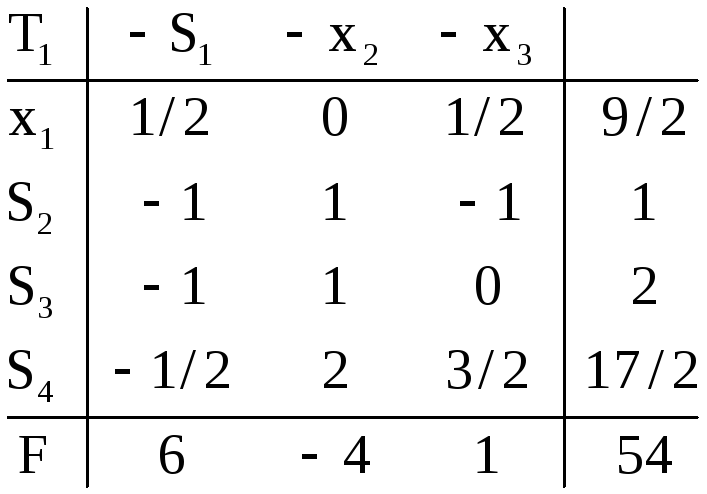
Таблица допустима и удовлетворяет условию строгой оптимальности. По критерию оптимальности- единственный оптимальный план и. В экономических терминах это означает, что максимальный доход равен 61 и достигается только одним способом – объемы производства трех видов продукции должны быть равны 4, 2 и 1(в соответствующих единицах). При этом ресурсы первых трех видов будут израсходованы полностью, а остаток четвертого ресурса составит три единицы.