Математика 2012-13 Бакалавры / 5_Практикум / ПРАКТИЧЕСКИЕ ЗАНЯТИЯ / Векторная алгебра

ПРАКТИЧЕСКИЕ

ЗАНЯТИЯ

«ВЕКТОРНАЯ АЛГЕБРА »

Занятие 1

Примеры решения задач

Задача 1. В равнобедренной трапеции ОАСВ угол ,,

- середина сторон ВС и АС. Выразить векторы через - единичные векторы направлений .

В М С

N

O A

Решение. . Так как . Найдем

вектор . Из треугольника ОСА , а так как , а

, вектор . Найдем из треуголь-

ника ONC , а так как , , .

Из треугольника OMN .

Задача 2. Даны векторы и , приложены к общей точке. Найти орт биссектрисы угла между .

Решение. Диагональ четырехугольника совпадает с биссектрисой, если этот четырехугольник – ромб (квадрат). Найдя , получим угол с одинаковыми по длине сторонами, равными единице. Таким образом, вектор направлен по биссектрисе угла между .

, ,

.

Найдем длину вектора , тогда орт биссектрисы равен .

Задача 3. Разложить вектор по трем некомпланарным векторам: .

Решение. . .

Приравняем коэффициенты справа и слева:

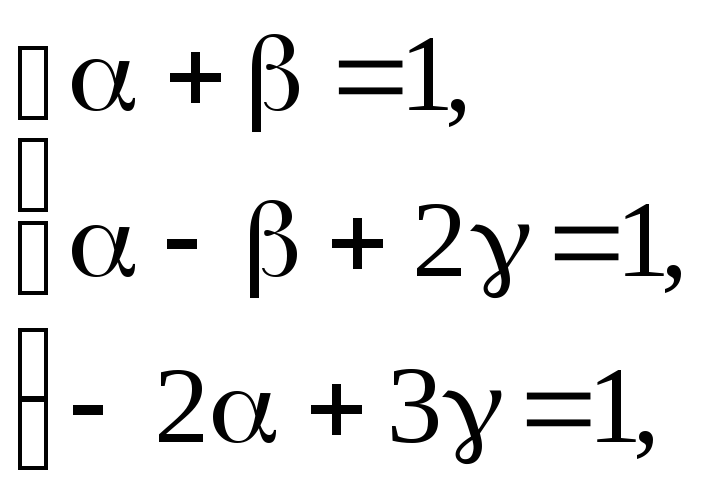тогда и .

Задача 4. Даны точки

Разложить вектор по ортам и найти его длину, направляющие косинусы, орт вектора .

Если известны координаты точек и , то координаты вектора

Разложение этого вектора по ортам :

Длина вектора находится по формуле а направляющие косинусы равны Орт вектора

Найдем координаты векторов:

и

Вектор

Занятие 2

Скалярное произведение векторов

Примеры решения задач

Задача 1. Определить длины диагоналей параллелограмма, построенного на векторах и , где таковы, что .

Решение. Диагонали параллелограмма есть векторы и . Вычислим длину вектора : .

Аналогично вычисляется длина вектора .

Задача 2. Найдите вектор , коллинеарный вектору и удовлетворяющий условию .

Решение. Обозначим вектор , тогда из условий задачи

или ,

тогда . Итак: .

Задача 3. Даны вершины треугольника Найти угол при вершине А и проекцию вектора на сторону АС. С

Внутренний угол при вершине А образован векторами ,

А В

Тогда

Проекция на направление вектора :

.

Задача 4. На материальную точку действуют силы . Найти работу равнодействующей этих сил при перемещении точки из положения в положение .

Решение. Найдем силу и вектор перемещения . , тогда искомая работа .

Занятие 3

Векторое произведения векторов. Смешанное произведение векторов

Примеры решения задач

Задача 1. Найти координаты векторного произведения , если , .

Решение. Найдем и . Векторное произведение, по определению, равно .

Задача 2. Силы и приложены к точке . Вычислить величину момента равнодействующей этих сил относительно точки .

Решение. Найдем силу и плечо : . Момент

сил вычисляется по формуле

, а его модуль .

Задача 3. Даны вершины треугольника Найти его площадь и длину высоты, опущенной из вершины С.

. Находим векторы

Векторное произведение

Так как где длина высоты, опущенной из вершины С на сторону АВ, .

Задача 4. Даны координаты вершин параллелепипеда: . Найти объем параллелепипеда, его высоту, опущенную из вершины С, угол между вектором AD и гранью, в которой лежат векторы АВ и АС.

Решение. По определению, объем параллелепипеда равен смешанному произведению векторов, на которых он построен. Найдем эти векторы:

.

Объем этого параллелепипеда .

С другой стороны, объем параллелепипеда , - это площадь параллелограмма: .

, тогда высота .

Угол между вектором и гранью найдем по формуле

.

так как вектор перпендикулярен грани, в которой лежат векторы . Угол между этим вектором и вектором находим по известной формуле

. Очевидно, что искомый угол .

Итак: .

Задача 5. Проверить, лежат ли в одной плоскости точки , . Найти линейную зависимость вектора , если это возможно.

Решение. Найдем три вектора: .

.

Три вектора лежат в одной плоскости, если они компланарны, т. е. их смешанное произведение равно нулю: . Следовательно, эти три вектора линей-

но зависимы. Найдем линейную зависимость от .

.

Решая эту систему, получим , т.е. .

Задача 6. При каком ненулевом значении t вектор будет еди-

ничным, если Вектор будет единичным, если его длина будет равна единице, т. е. .

Задача 7. Даны координаты вершин пирамиды ; .

1. Найти длину вектора .

2. Найти угол между векторами .

3. Найти проекцию вектора на вектор .

4. Найти площадь грани АВС .

5. Найти объем пирамиды ABCD.

Координаты векторов:

1. Длина вектора

2.

3. Проекция вектора на вектор

4.

5.

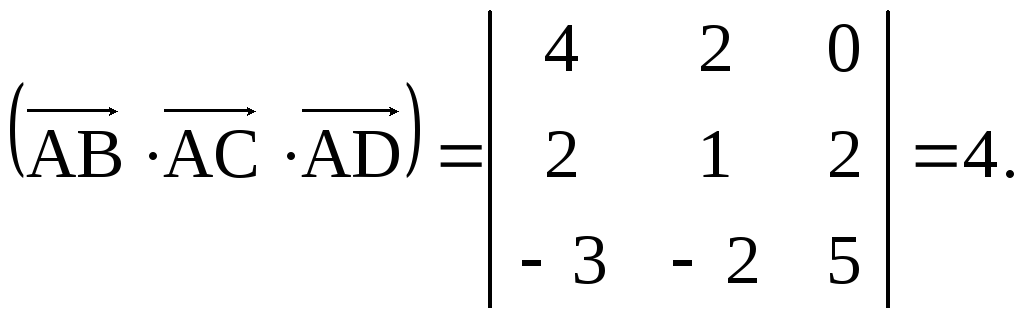
7