
Маршруты на графах
Пусть дан
неориентированный граф
![]() .
Маршрутом длины
.
Маршрутом длины![]() называется некоторая последовательность
называется некоторая последовательность![]() рёбер
рёбер![]() ,
такая, что вершины двух соседних рёбер
последовательности совпадают. Примерами
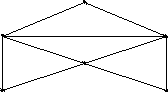
маршрутов на графе (рис.7) могут служить
следующие последовательности рёбер
,
такая, что вершины двух соседних рёбер
последовательности совпадают. Примерами
маршрутов на графе (рис.7) могут служить
следующие последовательности рёбер![]() и
и![]() .
Первый из этих маршрутов соединяет
.
Первый из этих маршрутов соединяет![]() с
с![]() .
Второй образует замкнутый маршрут,
проходя через
.
Второй образует замкнутый маршрут,
проходя через![]() ,
приводит в ту же вершину, из которой
начался.
,
приводит в ту же вершину, из которой
начался.
Две вершины графа
называются связанными, если существует
маршрут, соединяющий эти вершины. Граф,
любая пара вершин которого связана,
называется
связным графом. Граф
(рис. 7) не является связным, отсутствуют
маршруты из
![]() в
в![]() из
из![]() в
в![]() и т. д. Граф
и т. д. Граф![]() (рис. 11) является связанным, а его суграф
и подграф не являются связанными.
Маршрут, все рёбра которого различны,
называютсяцепью.
Цепь, проходящая через различные вершины,
называется простой (элементарной) цепью.
Замкнутая цепь называется циклом,
а цикл
проходящий через различные вершины –
простым
циклом. Так
в графе (рис.7)
маршрут
(рис. 11) является связанным, а его суграф
и подграф не являются связанными.
Маршрут, все рёбра которого различны,
называютсяцепью.
Цепь, проходящая через различные вершины,
называется простой (элементарной) цепью.
Замкнутая цепь называется циклом,
а цикл
проходящий через различные вершины –
простым
циклом. Так
в графе (рис.7)
маршрут
![]() является простой цепью, маршрут
является простой цепью, маршрут![]() циклом.
циклом.
На практике большое значение имеют задачи о нахождении различного рода маршрутов. Наиболее известные из них эйлеров и гамильтонов циклы.
Цикл, содержащий
все рёбра графа, называется эйлеровым,
а граф,
имеющий эйлеров цикл, называется
эйлеровым
графом. Если
эйлеров граф плоский, то его можно
изобразить одним росчерком пера (не
отрывая пера от бумаги), причем начальная
и конечная вершины совпадают. На рисунке
12 изображен граф обход всех рёбер
которого ровно один раз возможен по
маршруту:
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рисунок 12
Вопрос о существовании эйлерова графа разрешается следующей теоремой:
Теорема.
Конечный,
неориентированный граф является
эйлеровым тогда и только тогда, когда
он связный и степени всех его вершин
четны. Граф (рис. 12) эйлеров, т. к. он
связан, степени
![]()
![]()
![]() равны двум, а степени
равны двум, а степени![]()
![]() четырём.
четырём.
Простой цикл, который проходит через все вершины графа, называется гамильтоновым. Условий, гарантирующих существование в графе гамильтонова цикла, математиками пока не установлено.
Пример задачи на нахождение гамильтонова цикла. Задача коммивояжера
Пусть имеется несколько связанных между собой пунктов (городов). Выходя из фиксированного пункта, коммивояжер должен вернуться в него, посетив все пункты ровно один раз. Обычно задача усложняется введением дополнительного ограничения: например, пройти маршрут за самое короткое время или с минимальными затратами на транспорт. Отсутствие условий существования гамильтонова цикла приводит к тому, что, приступая к решению задачи неизвестно, имеет ли она вообще решение или нет. На рисунках 13 и 14 представлены соответственно граф, имеющий гамильтонов цикл, и не имеющий такового.
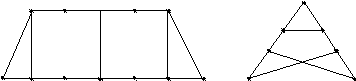
Рис. 13 Рис. 14
В ориентированном графе маршруты называются ориентированными: начальная вершина каждой последующей дуги маршрута должна совпадать с конечной вершиной предыдущей дуги. Если рассматривать изображение ориентированного графа, то движение по маршрутам на нём должно осуществляться только в направленияx, указанных стрелками. Маршрут, не содержащий повторяющихся дуг, называется путем. Путь, не содержащий повторяющихся вершин, называется простым путем. Замкнутый путь называется контуром. Простой контур – контур, не имеющий повторяющихся вершин. Если в графе содержится хотя бы один контур, то это контурный граф.
