З а д а ч а 7

Канонические уравнения прямой в пространстве имеют вид

, (9)

где - точка, лежащая на прямой, а- направляющий вектор прямой (ненулевой вектор, параллельный прямой).

Чтобы перейти от общих уравнений прямой

(10)

к ее каноническим уравнениям, нужно на прямой найти какую-нибудь точку и определить направляющий вектор прямой. Точкуможно найти так: задаем произвольно значение одной переменной, например,, и из общих уравнений прямой (10) найдем значения. Направляющий векторпараллелен

линии пересечения плоскостей (10) и, следовательно, перпендикулярен векторам . Поэтому в качествеможно взять вектор

.

Пример 7

Написать канонические уравнения прямой

Найдем точку , лежащую на прямой. Пусть.

Тогда

Решив систему, найдем . Таким образом,. Найдем направляющий вектор прямой

.

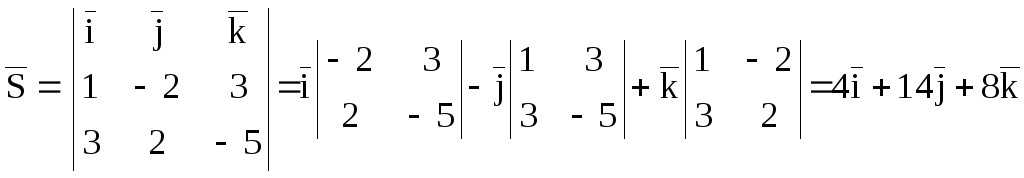Запишем канонические уравнения: .

З а д а ч а 8

Точка пересечения Р прямой и плоскости находится следующим образом: уравнения прямой приводят к параметрическому виду 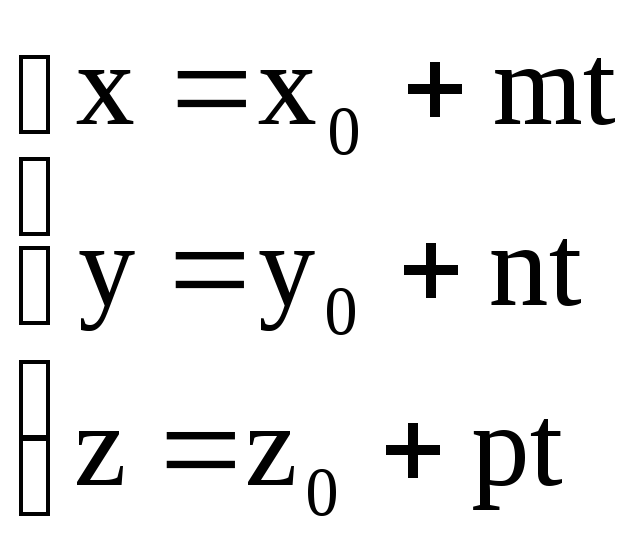, затем подставляют в уравнение плоскостии определяют значение параметраt , соответствующее точке пересечения. Если при такой подстановке уравнение плоскости выполняется при любом t, то прямая лежит в плоскости, а если не выполняется ни при каком t, то прямая параллельна плоскости. Найденное значение t подставляют в параметрические уравнения прямой.

Пример 8

Найти точку пересечения прямой и плоскости.

Приведем уравнения прямой к параметрическому виду:

; , т. е. параметрические уравнения прямой имеют вид

Подставив х, у, z в уравнение плоскости, найдем t:

.

Искомая точка пересечения прямой и плоскости имеет координаты

, т. е. .

З а д а ч а 9

Чтобы найти точку , симметричную точкеотносительно прямой, нужно найти проекцию точки М на прямую. Проекция будет серединой отрезка. Проекция есть точка пересечения прямой с перпендикулярной к ней плоскостью, проходящей через точку М. Так как векторперпендикулярен этой плоскости, ее уравнение запишем в виде

.

Далее, как и в предыдущей задаче, находим точку Р (точку пересечения данной прямой с найденной плоскостью). Зная середину отрезка , найдем координаты точки. Чтобы найти точку, симметричную точкеотносительно плоскости, нужно найти проекцию точки М на плоскость. Проекция будет серединой отрезка.

Проекция точки на плоскость будет точкой пересечения перпендикуляра к плоскости, проходящего через точку М, с самой плоскостью. Векторбудет направляющим вектором перпендикулярной прямой.

Далее, как и в задаче 9, находим точку пересечения перпендикуляра с данной плоскостью.

Зная середину отрезка , найдем координаты точки.

Пример 9

Найти точку , симметричную точкеотносительно плоскости.

Запишем канонические уравнения перпендикуляра к плоскости. Векторбудет направляющим вектором перпендикуляра

.

Параметрические уравнения прямой :Подставляя х, у,z из этих уравнений в данное уравнение плоскости, найдем значение t:

Точка Р пересечения прямой с плоскостью будет иметь координаты

т. е. .

Так как Р – середина отрезка и- координаты, так как если то

10