ПРАКТИЧЕСКИЕ ЗАНЯТИЯ

«ПРОИЗВОДНАЯ ФУНКЦИИ,

ТЕХНИКА ДИФФЕРЕНЦИРОВАНИЯ»

ПРОИЗВОДНАЯ ФУНКЦИИ

Пусть в некотором промежутке задана непрерывная функция . - заданная точка (рис.33).

Дадим аргументу приращение

, тогда функция получит прира-щение , это величина отрезка ВС (рис.33).

Отношение называется средней скоростью изменения фун-кции в промежутке

, а предел этого

У Д

В

Е

А

С

О а в х

Рис. 33

отношения, когда , называется производной функции в заданной точке . Таким образом, .

Замечание. Если не существует, то и производной тоже не существует.

Производную функции в произвольной точке х принято обозначать или , или . Если же точка 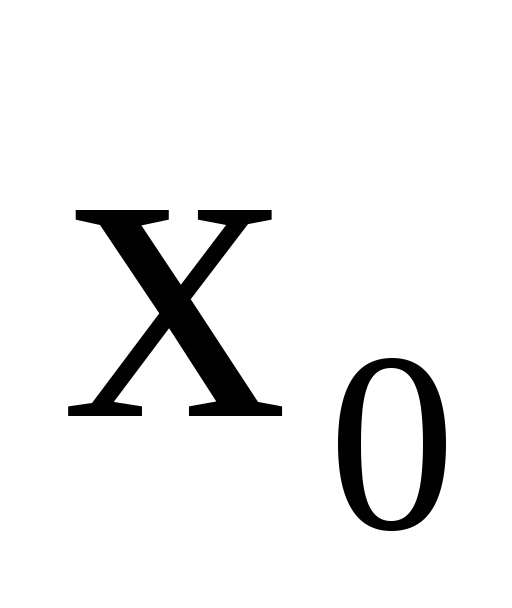задана, значение производной в этой точке записывают в виде , .

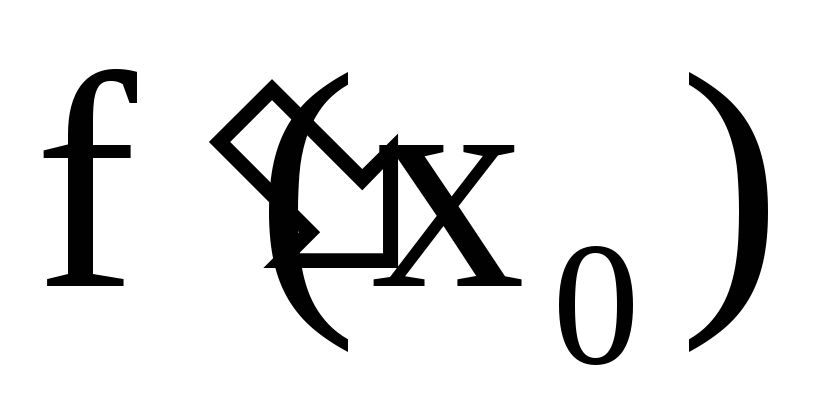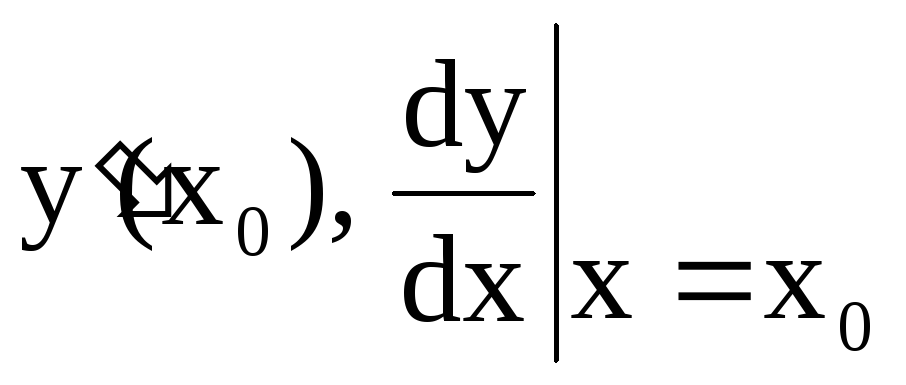Производная функции в заданной точке характеризует скорость изменения функции в этой точке. Например, производная от пути по времени есть скорость движения, то есть ; производная от скорости по времени дает ускорение движения . Если функция выражает количество электричества,

протекающего за время t через сечение проводника, то есть сила тока в момент времени t. Видно (рис. 33), что . Переходя к пределу при ,получаем . Итак, производная функции в заданной точке равна тангенсу угла , который образует касательная в точке с осью ОХ: . Так как , то . Поскольку уравнение прямой с угловым коэффициентом имеет вид , то получим уравнение касательной АД: (рис. 33).

Так как нормаль , то . Поэтому уравнение нормали АЕ имеет вид (рис. 33).

Пример. Найти производную функции в производной точке х.

Решение. , тогда . Так как , то

. .

.

Замечание. При нахождении предела следует помнить, что , -переменная.

Пример (самостоятельно). Пользуясь определением, найти производную функции . Ответ: .

Решение. Так как , то . Уравнение касательной или . Уравнение нормали или .

Пример. Написать уравнение касательной и нормали к кривой в точке А (2; 8) (рис.34).

у

в А Е

Д

О 1 2 х

Рис. 34

Основные правила дифференцирования

1. Производная константы равна нулю: .

2. Производная независимой переменной равна единице: .

3. Если функции и имеют производные в заданной точке х, то . .

4. Постоянный множитель можно выносить за знак производной: .

5. Если , где , то у – сложная функция. Тогда .

6. Если и - взаимно обратные функции, то .

Найти производные функций.

Пример. .

Пример. , .

Пример.,

.

Пример. . Это сложная функция .

Производные основных элементарных функций

Все последующие функции предполагаются сложными: .

1. Производные степенных функции:

; .

2. Производные показательных функций:

.

3. Производные логарифмических функций:

.

4. Производные тригонометрических функций:

.

5. Производные обратных тригонометрических функций:

.

Примеры.Найти производные функций

Пример 1. .

Пример 2. .

.

Пример 3. .

.

Пример 4. , .

Пример 5. .

.

Примеры для самостоятельного решения.

1. .

Указание. Каждое слагаемое записать в виде степенной функции с дробным показателем степени.

Ответ: .

2. . Ответ: .

3. . Ответ: .

4. . Ответ: .

5. . Ответ: .

6. . Ответ: .

7. . Ответ: .

8. . Ответ: .

Указание. Целесообразно предварительно выполнить логарифмирование .

Дифференцирование функций, заданных параметрически

Производная функции заданной параметрически, находится по формуле .

Пример. , .

Пример. . .

Примеры для самостоятельного решения.

1. .Ответ: . 2. 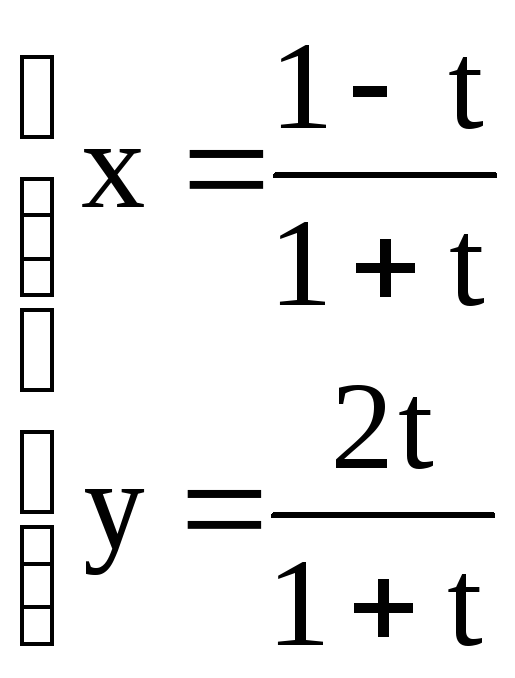. Ответ: .

3. . Ответ: . 4. . Ответ: .

7