3.5. Метод скорейшего спуска для случая линейной системы

Рассмотрим систему линейных уравнений:

с действительной матрицей и столбцом свободных членов. Тогдаи. И исходная система имеет вид:, где– невязка вектораи.

Соответственно, окончательно имеем:

.

Пример. Методом скорейшего случая решить систему уравнений:

Решение. В качестве начального приближения выберем .

Тогда ,

,

.

Вычисляя коэффициент , получим:.

Отсюда , причем невязка. Аналогично вычисляя, получим:;

;

;

.

Процесс скорейшего случая для линейных систем сходится медленно. Так, здесь точное решение: ;;;.

4. Приближение функций

4. 1. Метод наименьших квадратов

В инженерной деятельности часто возникает необходимость описать в виде функциональной зависимости связь между величинами, заданными таблично или в виде набора точек с координатами , где– общее количество точек. Как правило, эти табличные данные получены экспериментально и имеют погрешности.

Рис. 12

При аппроксимации желательно получить относительно простую функциональную зависимость (например, многочлен), которая позволила бы «сгладить» экспериментальные погрешности, вычислить значения функции в точках, не содержащихся в исходной таблице.

Эта функциональная зависимость должна с достаточной точностью соответствовать исходной табличной зависимости. В качестве критерия точности чаще всего используют критерий наименьших квадратов, т.е. определяют такую функциональную зависимость , при которойобращается в минимум. Погрешность приближения оценивается величиной. В качестве функциональной зависимости рассмотрим многочлен. Формула минимизируемой функции примет вид. Условия минимумаможно записать, приравнивая нулю частные производныепо всем переменным,.

Получим систему уравнений

или ,.

Эту систему уравнений перепишем в следующем виде:

, .

Введем обозначения: 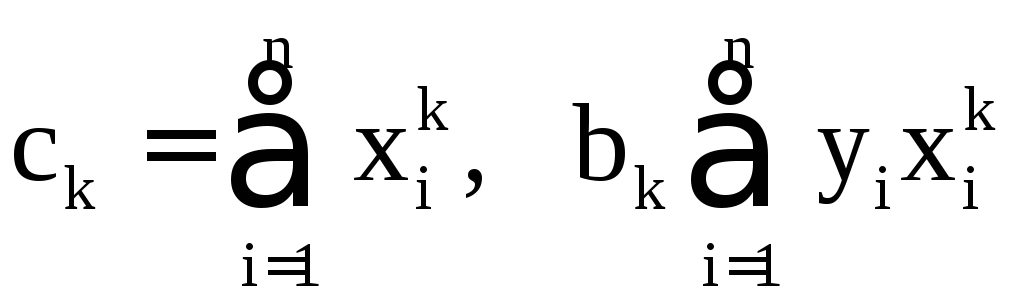. Последняя система может быть записана так:,.

Её можно переписать в развернутом виде:

.

Матричная запись системы имеет следующий вид: . Для определения коэффициентов, и, следовательно, искомого многочлена, необходимо вычислить суммыи решить последнюю систему уравнений. Матрицаэтой системы является симметричной и положительно определенной.

Погрешность приближения в соответствии с исходной формулой составит

. Рассмотрим частные случаи и.

Линейная аппроксимация .

.

;

, .

Отсюда система для нахождения коэффициентов имеет вид:

.

Её можно решить методом Крамера.

Квадратичная аппроксимация .

.

.

.

, .

Или в развёрнутом виде

Решение системы уравнений находится по правилу Крамера.

Пример. Построим по методу наименьших квадратов многочлены первой и второй степени и оценим степень приближения. Значения в точках,приведены в следующей таблице.

	1	2	3	4	5
	1	2	3	4	5
	-1	1	2	4	6

Вычислим коэффициенты по формулам для линейной и квадратичной аппроксимация;.

Для линейной аппроксимации система уравнений определения коэффициентов имногочлена первой степениимеет вид:

.

Решая эту систему, получим:

.

.

Для квадратичной аппроксимации система уравнений определения коэффициентов имногочлена второй степениимеет вид:

.

И коэффициенты равны:

. Тогда

.

Сравним значения, рассчитанные для функциональной зависимости, с исходными данными. Результаты приведены в табл. 3.

Таблица 3

	0	1	2	3	4
	1	2	3	4	5
	-1	1	2	4	6
	-1	0,7	2,4	4,1	5,8
	-1	0,62	2,24	4	6,9

Погрешность приближения в соответствии с исходными формулами составит:

.

.