1.8. Комбинированный метод

Пусть , аисохраняют постоянные знаки на отрезке. Соединяя методы хорд и касательных, получаем метод на каждом этапе, которого находим значения по недостатку и значения по избытку точного корняуравнения. Пусть– последовательные приближения метода хорд,– последовательные приближения метода касательных. Пошаговая иллюстрация представлена на рис. 11.

Возможны 4 случая: 1) , 2) ,

3) , 4),

которые можно свести к первому случаю.

y

x₀=а х₁ х₂

x^* х

Рис. 11

.

. .

Очевидно, что и.

По окончании процесса за значение корня лучше всего взять среднее арифметическое полученных значений:.

Пример. Вычислить положительный корень уравнения . Так как, то.

, на, поэтому.

.

.

; .

Так как , то

; .

Так как , то.

2. Решение систем линейных алгебраических уравнений

2.1. Постановка задачи

Требуется найти решение системы линейных уравнений:

или в матричной форме: , где

По правилу Крамера система линейных уравнений имеет единственное решение, если определитель системы отличен от нуляи значение каждого из неизвестных определяется следующим образом:, где– определитель матрицы, получаемой заме-

ной -го столбца матрицы столбцом правых частей .

Непосредственный расчет определителей для больших является очень трудоемким.

Известные в настоящее время многочисленные приближенные методы решения систем линейных алгебраических уравнений распадаются на две большие группы: прямые методы и методы итераций.

Прямые методы всегда гарантируют получение решения, если оно существуют, однако, для больших требуется большое количество операций, и возникает опасность накопления погрешностей.

Этого недостатка лишены итерационные методы, но зато они не всегда сходятся и могут применяться лишь для систем определенных классов.

Норма матрицы является некоторой обобщенной оценкой значений элементов матрицы. Для её вычисления можно использовать следующие выражения:

,

, .

2.2. Метод простой итерации

Для того чтобы применить метод простой итерации, необходимо систему уравнений

(1)

с квадратной невырожденной матрицей привести к виду

, (2)

где – квадратная невырожденная матрица с элементами,– вектор-столбец неизвестных, – вектор-столбец с элементами , . Существуют различные способы приведения системы (1) к виду (2). Рассмотрим самый простой.

Представим систему в развернутом виде:

(3)

Из первого уравнения системы (3) выразим неизвестную :

из второго уравнения – неизвестную :

и т. д. В результате получим систему:

(4)

Матричная запись системы (4) имеет вид (2). На главной диагонали матрицы находятся нулевые элементы, а остальные элементы вычисляются по формулам:

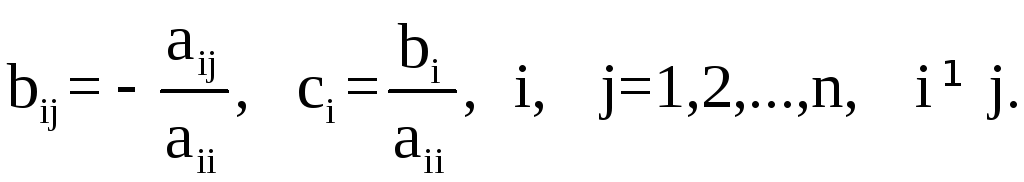(5)

Очевидно, что диагональные элементы матрицы должны быть отличны от нуля. Выберем произвольно начальное приближение. Обычно в качестве первого приближения берутили. Подставим начальное приближение в правую часть (4). Вычисляя левые части, получим значения . Продолжая этот процесс дальше, получим последовательность приближений, причем приближение строится следующим образом:

Последняя система представляет собой расчетные формулы метода простой итерации.

Сходимость метода простой итерации. Известно следующее достаточное условие сходимости метода простой итерации.

Если элементы матрицы удовлетворяют условию:

, (6)

то итерационная последовательность сходится к точному решению.

Условие (7) называют условием преобладания диагональных элементов матрицы , так как оно означает, что модуль диагонального элемента-ой строки больше суммы модулей остальных элементов этой строки,.

Необходимо помнить, что условие сходимости (6) является лишь достаточным. Его выполнение гарантирует сходимость метода простых итераций, но его невыполнение, вообще говоря, не означает, что метод расходится.

Справедлива следующая оценка погрешности:

, (7)

где .

Правую часть оценки (7) легко вычислить после нахождения очередного приближения.

Иначе достаточное условие (6) для матрицы может быть переформулирована так: если, то итерационный процесс (6) сходится к точному решению системы.

Критерий окончания. Если требуется найти решение с точностью , то в силу (7) итерационный процесс следует закончить, как только на-ом шаге выполнится неравенство:.

Поэтому в качестве критерия окончания итерационного процесса можно использовать неравенство , где.

Если выполняется условие , то можно пользоваться более простым критерием окончания:

. (8)

В других случаях использование последнего критерия (8) неправомерно и может привести к преждевременному окончанию итерационного процесса.

Пример 3.

Применим метод простой итерации для решения системы уравнений

.

Заметим, что метод простой итерации сходится, так как выполняется условие преобладания диагональных элементов:

, ,

, .

Пусть требуемая точность . Вычисления будем проводить с четырьмя знаками после десятичной точки.

Приведем систему к виду:

Величина равна 0,1179, т. е. выполняется условиеи можно пользоваться критерием окончания итерационного процесса (8). В качестве начального приближения возьмем элементы столбца свободных членов:. Вычисления будем вести до тех пор, пока все величины,, а следовательно, ине станут меньше.

Последовательно вычисляем:

при

при

.

при

.

при

.

Вычисляем модули разностей значений при и :

. Так как все они больше заданной точности , продолжаем итерации.

При

.

Вычисляем модули разностей значений при и:

. Все они меньше заданной точности , поэтому итерации заканчиваем. Приближенным решением системы являются следующие значения:

.

Для сравнения приведем точные значения переменных:

.