
- •Численные методы
- •Введение
- •1. Решение нелинейных уравнений
- •Постановка задачи
- •1.2. Основные этапы отыскания решения
- •1.3. Метод половинного деления
- •1.4. Метод простой итерации
- •Приведение уравнения к видудля обеспечения выполнения неравенства
- •1.5. Метод Ньютона (метод касательных)
- •1.6. Видоизменённый метод Ньютона
- •1.7. Метод хорд
- •1.8. Комбинированный метод
- •Решение систем линейных алгебраических уравнений
- •2.1. Постановка задачи
- •2.2. Метод простой итерации
- •2.3. Метод Зейделя
- •3. Решение систем нелинейных уравнений
- •3.1. Постановка задачи
- •3.2. Метод Ньютона для системы нелинейных уравнений
- •3.3. Метод итерации для нелинейной системы уравнений
- •3.4. Метод скорейшего спуска решения нелинейных систем
- •3.5. Метод скорейшего спуска для случая линейной системы
- •4. Приближение функций
- •4. 1. Метод наименьших квадратов
- •4.2. Построение интерполяционных многочленов
- •Многочлен Лагранжа
- •Многочлен Ньютона с конечными разностями
- •5. Вычисление собственных значений матрицы Методом Данилевского
- •6. Вычисление определённых интегралов. Метод симпсона (метод парабол)
- •7. Численное решение дифференциальных уравнений
- •7.1. Постановка задачи Коши
- •7.2. Метод Эйлера
- •7.3. Модифицированные методы Эйлера
- •7.4. Метод Рунге – Кутта
- •Решение краевой задачи для линейного дифференциального уравнения второго порядка методом прогонки
- •Приложение
- •Библиографический список
- •Оглавление
- •3.2. Метод Ньютона для системы нелинейных уравнений 26
- •3.3. Метод итерации для нелинейной системы уравнений 30
1.5. Метод Ньютона (метод касательных)
Метод
Ньютона является наиболее эффективным
методом решения нелинейных уравнений.
Пусть корень
![]() ,
т. е.
,
т. е.![]() .
Предполагаем, что функция
.
Предполагаем, что функция![]() непрерывна на отрезке
непрерывна на отрезке![]() и дважды непрерывно дифференцируема
на интервале
и дважды непрерывно дифференцируема
на интервале![]() .
Положим
.
Положим![]() .
Проведем
касательную к графику функции
.
Проведем
касательную к графику функции
![]() в точке
в точке![]() (рис. 8).
(рис. 8).
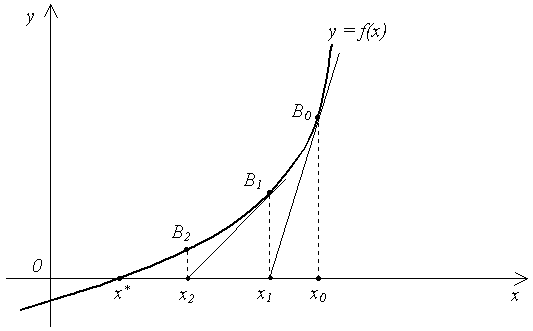
Рис. 8
Уравнение
касательной будет иметь вид:
![]() .
.
Первое
пересечение получим, взяв абсциссу
точки пересечения этой касательной с
осью
![]() ,
т. е. положив
,
т. е. положив![]() :
: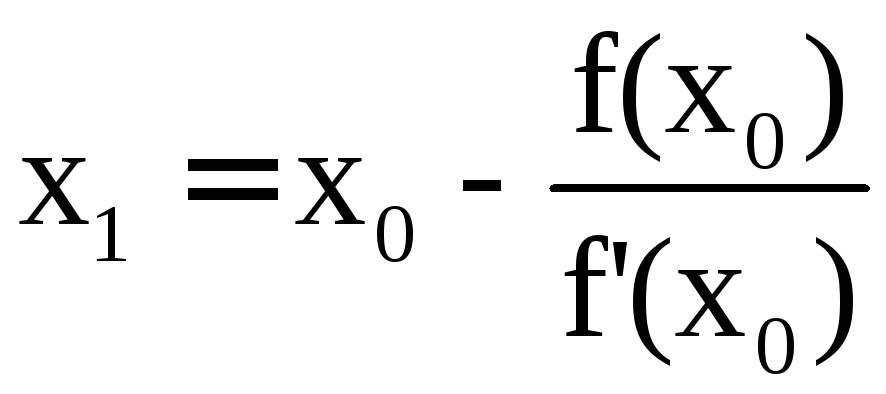 .
.
Аналогично
поступим с точкой
![]() ,
затем с точкой
,
затем с точкой![]() и т. д., в результате получим последовательность
приближений
и т. д., в результате получим последовательность
приближений![]() ,
причем
,
причем
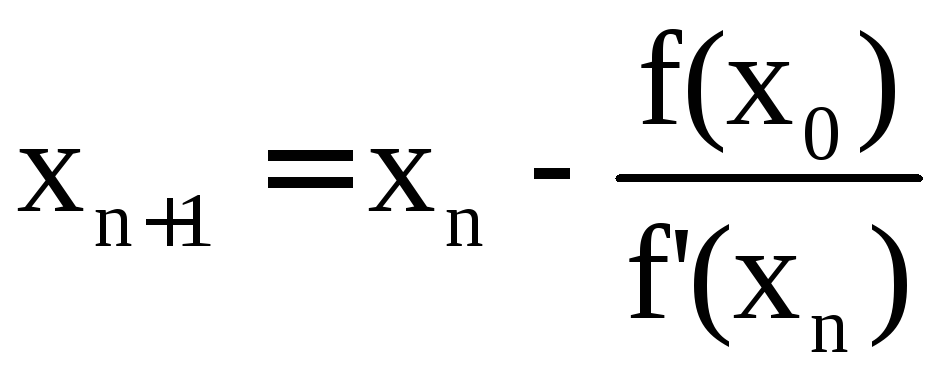 .
(6)
.
(6)
Формула (6) является расчетной формулой метода Ньютона.
Метод
Ньютона можно рассматривать как частный
случай метода простых итераций, для
которого
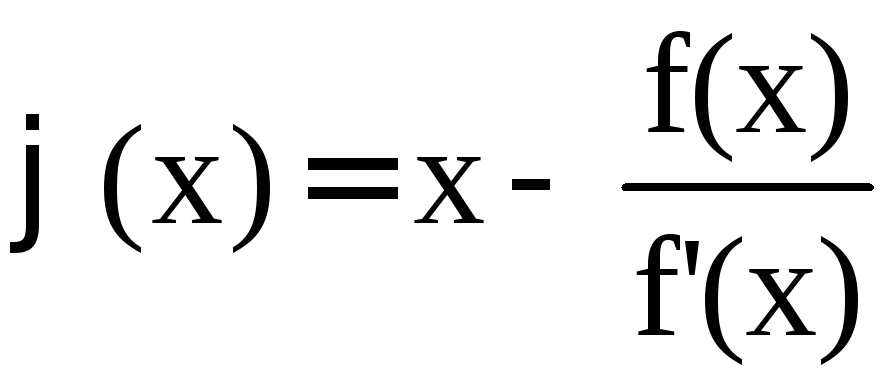 .
.
Сходимость метода. Сходимость метода Ньютона устанавливает следующая теорема.
Теорема.
Пусть
![]() – простой корень уравнения
– простой корень уравнения![]() и в некоторой окрестности этого корня
функция
и в некоторой окрестности этого корня
функция![]() дважды
непрерывно дифференцируема. Тогда
найдется такая малая
дважды
непрерывно дифференцируема. Тогда
найдется такая малая
![]() – окрестность корня
– окрестность корня![]() ,
что при произвольном выборе начального
приближения
,
что при произвольном выборе начального
приближения![]() из
этой окрестности итерационная
последовательность, определенная по
формуле (6) не выходит за пределы этой
окрестности и справедлива оценка:
из
этой окрестности итерационная
последовательность, определенная по
формуле (6) не выходит за пределы этой
окрестности и справедлива оценка:
![]() ,
(7)
,
(7)
где
![]() .
.
Сходимость метода Ньютона зависит от того, насколько близко к корню выбрано начальное приближение.
Выбор
начального приближения.
Пусть
![]() – отрезок, содержащий корень. Если в
качестве начального приближения
– отрезок, содержащий корень. Если в
качестве начального приближения![]() выбрать
тот из концов отрезка, для которого
выбрать
тот из концов отрезка, для которого
![]() ,
то итерации (6) сходятся, причем монотонно.
Рис. 8 соответствует случаю, когда в
качестве начального приближения был
выбран правый конец отрезка:
,
то итерации (6) сходятся, причем монотонно.
Рис. 8 соответствует случаю, когда в
качестве начального приближения был
выбран правый конец отрезка:![]() (Здесь
(Здесь![]() ).
).
Погрешность метода. Оценка (7) неудобна для практического использования. На практике пользуются следующие оценки погрешности:
![]() .
(8)
.
(8)
Критерий
окончания.
Оценка (8) позволяет сформулировать
следующий критерий окончания итераций
метода Ньютона. При заданной точности
![]() вычисления нужно вести до тех пор, пока
не будет выполнено неравенство
вычисления нужно вести до тех пор, пока
не будет выполнено неравенство
![]() .
.
Пример.
Вычислить методом Ньютона отрицательный
корень уравнения
![]() с точностью до 0,0001. Проведя отделение
корня, можно убедиться, что корень
локализован на интервале
с точностью до 0,0001. Проведя отделение
корня, можно убедиться, что корень
локализован на интервале![]()
![]()
![]() .
В этом интервале
.
В этом интервале![]() и
и![]() .
Так как
.
Так как![]() и
и![]() ,
то за начальное приближение можно
принять
,
то за начальное приближение можно
принять![]() .
.
|
|
|
|
|
|
-11 |
3453 |
-5183 |
0,6662 |
|
-10,3336 |
307,3 |
4276,8 |
0,0718 |
|
-10,2618 |
3,496 |
4185,9 |
0,0008 |
|
-10,261 |
0,1477 |
- |
- |
![]() .
Поэтому
.
Поэтому
![]() .
.
1.6. Видоизменённый метод Ньютона
Если
производная
![]() мало изменяется на отрезке
мало изменяется на отрезке![]() ,
то в расчетной формуле метода можно
положить:
,
то в расчетной формуле метода можно
положить:![]() .
Отсюда для корня
.
Отсюда для корня![]() уравнения
уравнения![]() получаем последовательные приближения
получаем последовательные приближения
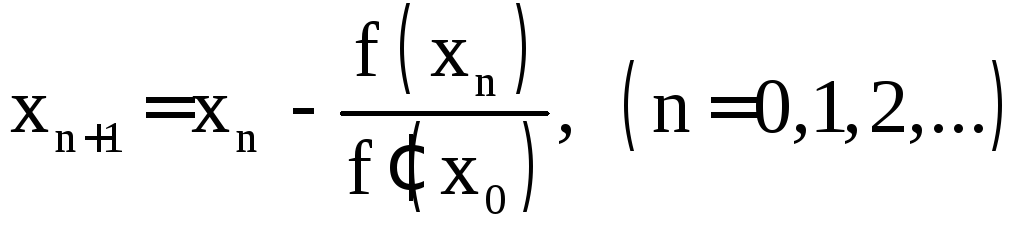 .
.
Геометрически
этот способ означает, что касательные
заменяются прямыми, параллельными
касательной к кривой
![]() ,
в ее фиксированной точке
,
в ее фиксированной точке![]() .
Этот способ избавляет от необходимости
вычислять каждый раз значения производной,
поэтому эта формула полезна, если
.
Этот способ избавляет от необходимости
вычислять каждый раз значения производной,
поэтому эта формула полезна, если![]() сложна.
сложна.
1.7. Метод хорд
Рассмотрим
еще одну модификацию метода Ньютона.
Пусть известно, что простой корень
![]() уравнения
уравнения![]() находится на отрезке
находится на отрезке![]() ,
то есть
,
то есть![]() .
И предположим, что
.
И предположим, что![]() при
при![]() (если это не так, то будем рассматривать
уравнение
(если это не так, то будем рассматривать
уравнение![]() ).
Заменим кривую
).
Заменим кривую![]() хордой
хордой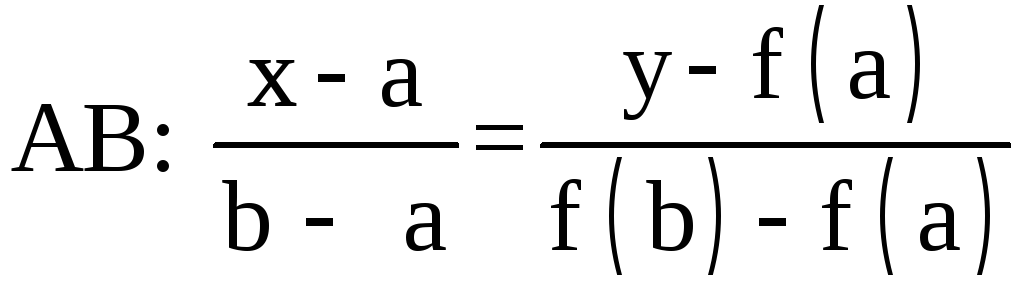 .
.
А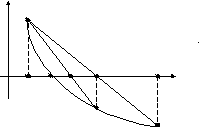
х2 х1 b = x0
а х* x
В
Рис. 9
y
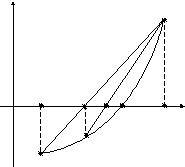
B
а = х0 х1 х2 b
х* x
А
Рис. 10
Возможны
два случая: 1)
![]() (рис. 9); 2)
(рис. 9); 2)![]() (рис. 10). В первом случае конец
(рис. 10). В первом случае конец![]() неподвижен
и последовательные приближения:
неподвижен
и последовательные приближения:
![]()
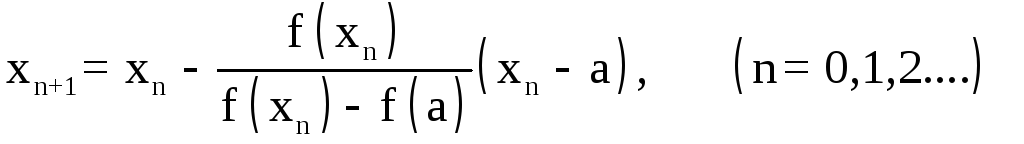 (9)
(9)
образуют
ограниченную монотонно убывающую
последовательность, причем
![]() .
.
Во
втором случае неподвижен конец
![]() ,
а последовательные приближения:
,
а последовательные приближения:![]()
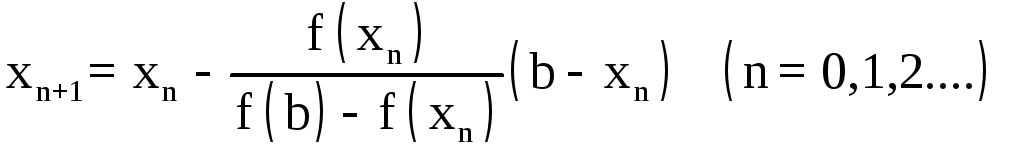 (10)
(10)
образуют
ограниченную монотонно убывающую
последовательность, причем
![]() Итак, в результате получаем следующее
Итак, в результате получаем следующее
Выбор начального условия:
1.
Рассматриваем только случай
![]() (иначе
(иначе![]() ).
).
2.
Начальное приближение x0
выбираем
из условия
![]()
![]()
Неподвижен тот конец, для которого знак функции совпадает со знаком ее второй производной.
Критерий
окончания.
Критерий окончания итераций метода
хорд такой же, как и для метода Ньютона.
При заданной точности
![]() вычисления нужно вести до тех пор, пока
не будет выполнено неравенство
вычисления нужно вести до тех пор, пока
не будет выполнено неравенство![]() .
.
Пример.
Найти положительный корень уравнения
с точностью
![]()
![]() .
Отделим корень. Так как
.
Отделим корень. Так как![]() ,
,![]() ,
то
,
то![]() .
Разделим интервал пополам:
.
Разделим интервал пополам:![]() ,
тогда
,
тогда![]() .
.
Найдём
производные:
![]() ,
,![]() .
Исходя из того, что
.
Исходя из того, что![]() ,
то
,
то![]() и пользуемся формулой (10):
и пользуемся формулой (10):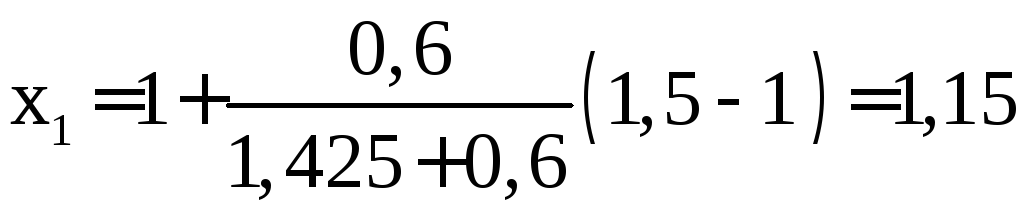 ,
,![]() .
.
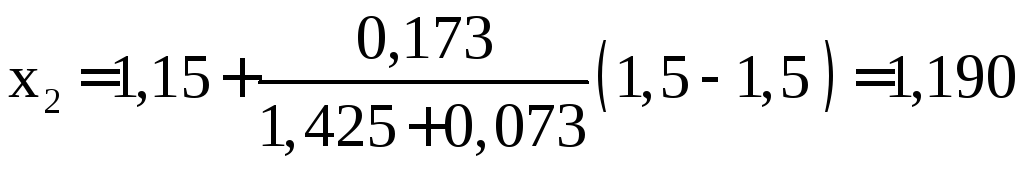 ,
,
![]() ,
,![]() .
.
Так
как
![]() ,
то
,
то![]() .
.
