
Математика 2012-13 Бакалавры / 5_Практикум / ПРАКТИЧЕСКИЕ ЗАНЯТИЯ / Комплексные числа
.docКОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
Комплексными
числами
называются числа вида
![]() ,
где
,
где
![]() – действительные числа,
– действительные числа,
![]() – действительная часть,
– действительная часть,
![]() – мнимая часть комплексного числа.
– мнимая часть комплексного числа.
По определению,
два комплексных числа:
![]() и
и
![]() – равны тогда и только тогда, когда
– равны тогда и только тогда, когда
![]() и
и
![]() .
.
Комплексное
число
![]() называется сопряженным комплексному
числу
называется сопряженным комплексному
числу
![]() ,
если
,
если
![]() .
Другими словами, если
.
Другими словами, если
![]() ,
то
,
то
![]() .
.
Всякому
комплексному числу
![]() можно поставить в соответствие
единственную точку плоскости
можно поставить в соответствие
единственную точку плоскости
![]() и обратно, всякую точку
и обратно, всякую точку
![]() плоскости
плоскости
![]() можно рассматривать как геометрический
образ единственного комплексного числа
можно рассматривать как геометрический
образ единственного комплексного числа
![]() .
.
|
М
0 х Рисунок 1
|
Для
сокращения вместо “точка, соответствующая
комплексному числу
|
нат, изображает действительное число нуль. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
В некоторых
случаях удобно считать геометрическим
изображением числа
![]() радиус-вектор точки
радиус-вектор точки
![]() –
–
![]() .
.
|
0 z3 5 x -2 z2
-5 z1 Рисунок 2 |
Пример 1.
Построить точки
В дальнейшем, наряду с представлением комплексных чисел в декартовых координатах, полезно иметь их представление в обобщенных полярных координатах. Рассмотрим
число
|
|
y M(x; y) ρ
φ 0 x Рисунок 3 |
Тогда
Полярный
радиус
|
Полярный угол
![]() называется аргументом
комплексного
числа и обозначается
называется аргументом
комплексного
числа и обозначается
![]() .
Тогда
.
Тогда
![]() .
.
Эта форма называется тригонометрической формой комплексного числа.
Модуль комплексного
числа определяется однозначно:
![]() .
.
Аргумент
комплексного числа определяется с
точностью до слагаемого, кратного
![]() .
Главным значением аргумента называется
значение, заключенное в интервале
.
Главным значением аргумента называется
значение, заключенное в интервале
![]() .
Обозначается оно
.
Обозначается оно
![]() .
Таким образом,
.
Таким образом,
![]() .
.
Очевидно,
![]() .
.
Главное значение аргумента определяется однозначно.
Так как
![]() ,
,

Тригонометрическая форма комплексного числа будет иметь вид
![]() .
.
Пример 2.
Написать в тригонометрической форме
комплексное число
![]() .
.
|
z 1
-1 0 x
Рисунок 4 |
Решение.
|
Пусть
![]() .
Используя формулу Эйлера
.
Используя формулу Эйлера
![]() ,
получаем так называемую показательную
форму записи
комплексного числа:
,
получаем так называемую показательную
форму записи
комплексного числа:
![]() .
.
Пример 3.
Представить в показательной форме
комплексное число
![]() .
.
|
-1 0 x
z -1 Рисунок 5 |
Решение
|
Пример 4.
Вычислить
![]() .
.
Решение.
По формуле Эйлера
![]() .
.
АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМ
Сложение и
умножение
комплексных чисел производится по
правилам сложения и умножения
алгебраических многочленов с учетом
![]() .
При записи результата следует отделить
действительную часть от мнимой, т. е.
собрать отдельно члены, содержащие
множитель
.
При записи результата следует отделить
действительную часть от мнимой, т. е.
собрать отдельно члены, содержащие
множитель
![]() ,
и члены, не содержащие множитель
,
и члены, не содержащие множитель
![]() :
:
![]()
![]()
![]()
В частности,
![]() .
Операции сложения и вычитания сводятся
к сложе- нию и вычитанию векторов,
изображающих эти числа. Отсюда расстояние
между точками
.
Операции сложения и вычитания сводятся
к сложе- нию и вычитанию векторов,
изображающих эти числа. Отсюда расстояние
между точками
![]() .
.
|
y
z1 z1+z2
z2 z1-z2
Рисунок 6 |
Пример 5.
Деление на комплексное число, отличное от нуля, определяется как действие, обратное умноже- нию. Для представления частного в виде
следует провести простые преобразования, показанные на следующем примере.
|
Пример 6.
 .
.
Для модуля и аргумента произведения и частного справедливы следующие утверждения:
1.
![]()
Пример 7.
Найти модуль и аргумент произведения
![]() .
.
Решение.
 .
.
Таким образом,
умножение на
![]() соответствует повороту вектора
соответствует повороту вектора
![]() на угол
на угол
![]() ;
;
2.
 .
.
Пусть
![]() .
.
Тогда
![]() .
.
Можно доказать
методом полной математической индукции,
что для любого целого
![]() (формула Муавра). Формула справедлива
и для целых отрицательных
(формула Муавра). Формула справедлива
и для целых отрицательных
![]() .
.
Пример 8.
Вычислить
![]() .
.
|
0 x
-1 z Рисунок 7 |
Решение
|
 ,
,

 .
.
Корнем
![]() -й
степени из комплексного числа называется
такое число
-й
степени из комплексного числа называется
такое число
![]() ,
для которого
,
для которого
![]() .
.
Используя формулу Муавра, получим
![]()
Для других
значений
![]() аргументы будут отличаться от полученных
на число кратное
аргументы будут отличаться от полученных
на число кратное
![]() ,
и, следовательно, получатся значения
корня, совпадающие с рассмотренными.
Итак, корень
,
и, следовательно, получатся значения
корня, совпадающие с рассмотренными.
Итак, корень
![]() -й
степени из комплексного числа имеет
-й
степени из комплексного числа имеет
![]() различных значений.
различных значений.
Пример 9.
Найти все значения
![]() и построить их.
и построить их.
|
Рисунок 8 |
Решение.
|
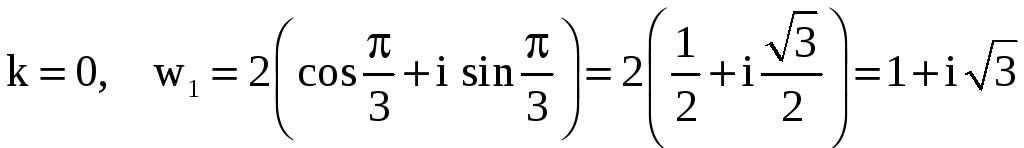 ,
,
 ,
,
 .
.

 y
y y
y
 y
y .
. y
y
 y
y ,
, y
y
 ,
,