4. Дифференциальные уравнения второго порядка

Дифференциальное уравнение второго порядка (д.у. II) содержит вторую производную некоторой функции, саму эту функцию, независимую переменную и первую производную. Д.у. II может быть записано в виде

или

Определение. Общим решением д.у.II называется функция зависящая от двух произвольных постоянных, такая, что

1. она удовлетворяет уравнению при любых значениях постоянных

2. каковы бы ни были начальные условия , можно найти такие значенияпри которых функцияудовлетворяет этим условиям.

Определение. Всякая функция, полученная из общего решения при конкретных значениях постоянных , называется частным решением д.у.II.

Заметим, что начальные условия для д.у. II представляют собой заданные значения функции и ее производной при одном и том же данном значении независимой переменнойИх обычно записывют

или т. е. задать начальные условия для нахождения частного решения д.у.II– значит задать три числа:

Пример. Дано д.у.II . Проверим, что его общим решением является функция

Найдем первую и вторую производные этой функции

Подставив в данное уравнение, получим

или

–

верное равенство. Найдем частное решение этого уравнения при заданных начальных условиях Подставим эти условия в выраженияy и

или

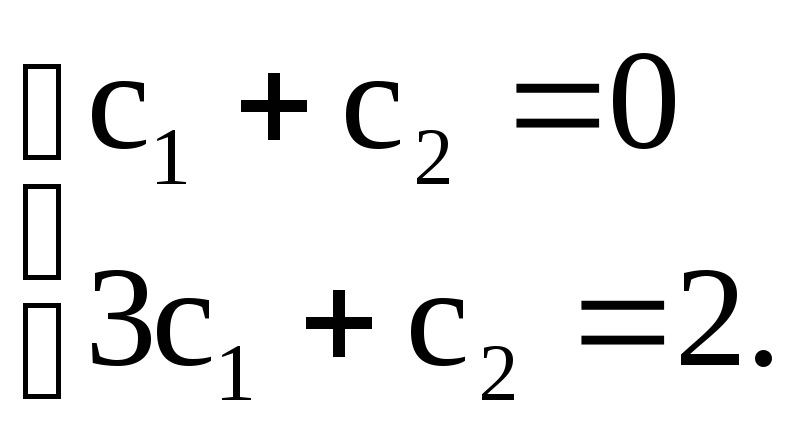
Решив эту систему, получим значения постоянных при которых из общего решениявыделим искомое частное решение

Рассмотрим некоторые типы дифференциальных уравнений второго порядка и способы их решения.

5. Дифференциальные уравнения второго порядка, допускающие понижение порядка

Рассмотрим некоторые типы д.у. II, решение которых сводится к решению дифференциальных уравнений первого порядка.

1-й тип. Простейший тип таких уравнений – это Дифференциальное уравнение содержит только вторую производную и некоторую функцию от х

(ни сама функция y, ни ее первая производная в уравнение не входят). Уравнение вида решается последовательным интегрированием два раза.

Пример 1.

Получили уравнение первого порядка

отсюда

^–

общее решение исходного уравнения (содержит две произвольные постоянные

и ).

Аналогично решаются и дифференциальные уравнения порядков выше второго, если они имеют такой же вид, например:

Пример 2.

–

общее решение данного уравнения.

Пример 3.

–

общее решение уравнения. Обратите внимание, общее решение дифференциального уравнения третьего порядка содержит три произвольные постоянные , а дифференциального уравнения четвертого порядка – уже четыреДопускают понижение порядка и дифференциальные уравнения вида

2-й тип. т. е. уравнения, в которые явно не входит сама искомая функцияу. Решаются такие уравнения подстановкой гдевспомогательная функция. ТогдаПодставивв данное уравнение, получим уравнение – дифференциальное уравнение первого порядка.

Пример 4. Решить уравнение

(9)

Положим и уравнение примет вид

–(10)

это линейное уравнение первого порядка относительно функции

Решаем его подстановкой где

Получим

Функция

Исходное уравнение (9) решалось подстановкой Поэтому

Интегрируя, получим –

общее решение уравнения (9).

Пример 5. Найти частное решение уравнения удовлетворяющее начальным условиямПрименим подстановку

Получим уравнение .

Это уравнение первого порядка с разделяющимися переменными относительно функции р. Разделим переменные:

Интегрируя, получим

Откуда

Используем второе начальное условие получим

Следовательно,

а после интегрирования

Применим первое начальное условие получим

Искомым частным решением будет

Еще одним типом уравнений, допускающих понижение порядка, является уравнение вида

3-й тип

т. е. уравнение, не содержащее явно независимую переменную х. Здесь порядок уравнения понижается на единицу путем следующей замены:

где

Здесь р – новая вспомогательная функция, а у играет роль независимой переменной. Тогда т. е.

Заметим, что вторая производная получена по правилу дифференцирования сложной функции.

Подставив выражения в данное уравнение, получим

–

уравнение первого порядка относительно р как функции от у.

Пример 6. Найти общее решение уравнения

(11)

Полагаем получим– (12)

это уравнение первого порядка с разделяющимися переменными. Приведя его к

виду и интегрируя, получим

Так как исходное уравнение (11) решалось с помощью подстановки получимдифференциальное уравнение с разделяющимися переменными относительно искомой функцииу от х .

Но так как произвольные постоянные, также произвольные постоянные. Поэтому полученный общий интеграл данного дифференциального уравнения можно записать в виде

т.е.

или

Пример 7. Найти частное решение уравнения при начальных условияхПрименим подстановкуТогда

Получим уравнение первого порядка:

Разделив уравнение на получим

Это линейное уравнение первого порядка относительно функции

Решаем его подстановкой

Тогда

Интеграл справа берем по частям с помощью подстановки

Тогда

Таким образом,

Тогда функция

Таким образом, , или

Найдем значение из начальных условий

Таким образом

Заметим, что константа может быть обозначена какс, т. к. – произвольная константатоже произвольная постоянная. Таким образом,

Найдем с из первого начального условия

Искомое частное решение имеет вид