Линейные дифференциальные уравнения первого порядка

Определение. Линейным уравнением первого порядка называется уравнение, линейное относительно искомой функции и ее производной. Общий вид линейного д.у.1: непрерывные функции или постоянные. Если, то уравнениерешается как дифференциальное уравнение с разделяющимися переменными.

Рассмотрим уравнения:

1) Это уравнение является линейным по определению

,но лучше рассматривать его как уравнение с разделяющимися переменными:

2) Это уравнение не является линейным, т. к. функцияy в уравнении имеет не первую степень, а выше

3)

Уравнение является линейным по определению. Но проще рассматривать его как однородное д.у.1: где– однородная функция нулевого измерения.

4) Запишем уравнение в виде. Это линейное д.у.1.

Решение линейного дифференциального уравнения первого порядка

Общее решение ищется в виде гденекоторые функции.

Покажем на примере, что любую функцию можно представить в виде произведения двух функций, одна из которых выбирается произвольно, а вторая зависит от этого выбора.

Пусть . Можнопредставить в виде различных пар множителей:

где первый множитель выбирается произвольно.

Указанная подстановка приводит линейное д.у.1 к решению двух д.у. с разделяющимися переменными. Покажем это в общем виде. В линейное уравнениеподставимПолучим

или

. (4)

Выберем функцию u   такой, чтобы

(5)

Уравнение (5) – дифференциальное уравнение с разделяющимися переменными:

Интегрируя, найдем функцию без

учета произвольной постоянной. Подставим найденную функцию в уравнение (4) и получимдифференциальное уравнение с разделяющимися переменными (3). Его общее решение позволит получить второй множитель

Тогда общее решение линейного д. у. 1.

Пример 1. Найти общее решение уравнения

Решаем подстановкой

(6)

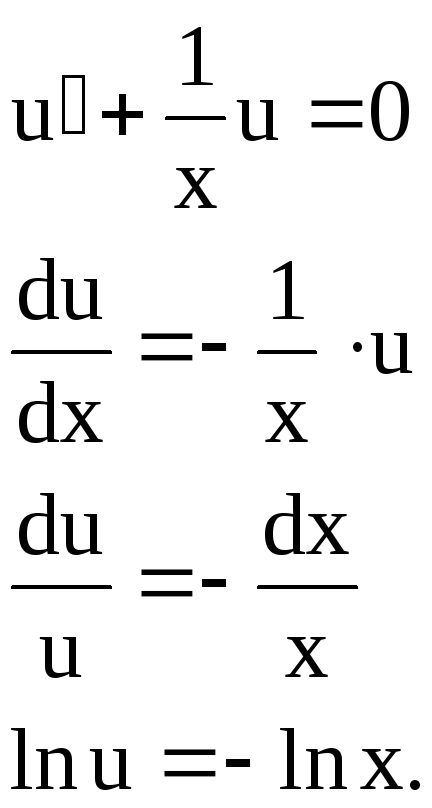
подставим в (6).

Общее решение:

Пример 2. Найти частное решение дифференциального уравнения

Подстановка: .

(7)

Подставим найденную функцию u в уравнение (7):

Таким образом, общее решение данного уравнения будет иметь вид

или

Найдем частное решение дифференциального решения, удовлетворяющее начальному условию

Следовательно, искомое частное решение такое:

Уравнения, приводящиеся к линейным (уравнения Бернулли)

Уравнение вида называется уравнением Бернулли. Здесь n – действительное число, причем при n = 0 получим линейное уравнение; при получим уравнение с разделяющимися переменными. Приуравнение Бернулли приводится к линейному, поэтому решается подстановкой

Пример. Найти общее решение уравнения

Разделив левую и правую части уравнения на х, представим его в виде

. Можно утверждать, что это уравнение имеет общий вид

т. е. является уравнением Бернулли. Решаем его подстановкой

где – вспомогательные функции.

Подставим в исходное уравнение:

(8)

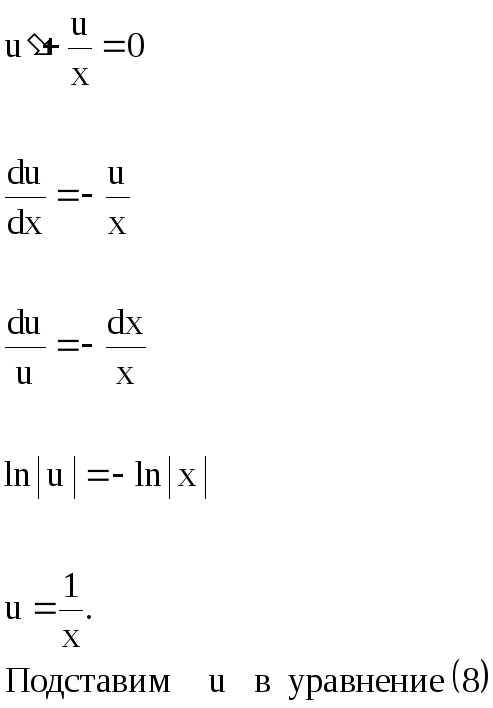
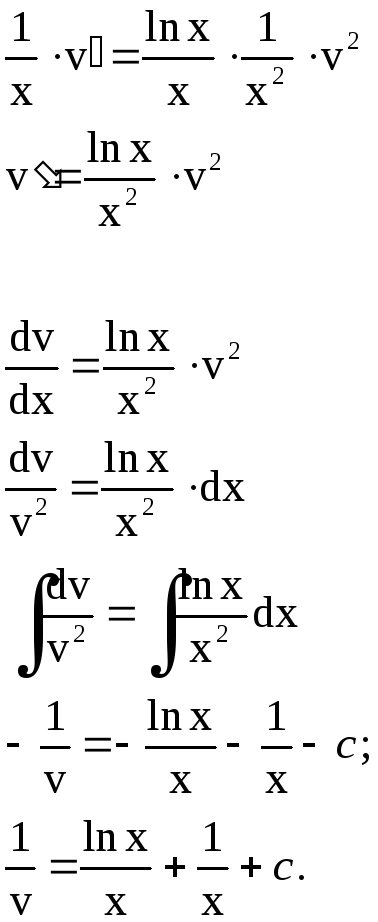
Для получения общего интеграла найдем

или

.

Замечание. Неопределенный интеграл найден с применением

формулы интегрирования по частям:

Производим подстановку

;.

Тогда