Решить самостоятельно

, .

Выше были рассмотрены основные приемы и формулы для нахождения неопределенных интегралов. Следует отметить, что многие функции не интегрируются в конечном виде. Так, например, функция непрерывна в промежутке, однако, интеграл от нее(интегральный синус) не выражается в конечном виде через элементарные функции. То же самое относится к

интегралам (интегральный косинус),(интегральный

логарифм).

Замечание. Во многих случаях заданный интеграл может быть найден различными способами. Так, например, интегралс помощью подстановкидает, где,. С другой стороны, если возьмем подстановку, то.

Поэтому .

Окончательно . Этот результатлишь формой отличается от предыдущего, так как

.

Занятие № 7. Контрольная работа

Вариант 1	Вариант 2
1. .	1. .
2. .	2. .
3. .	3. .
4. 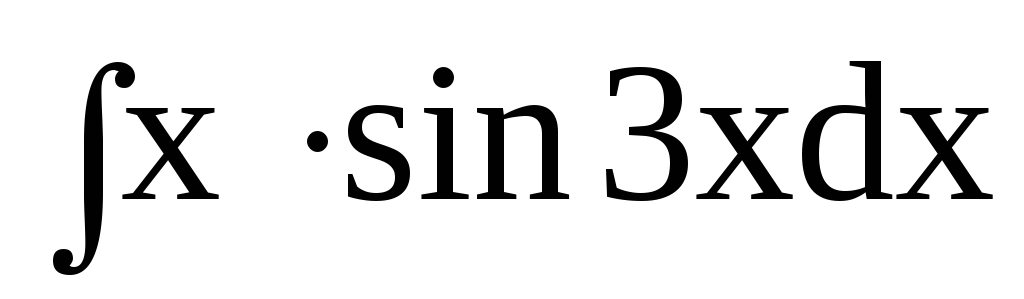.	4. .
5. .	5. .
6. .	6. .
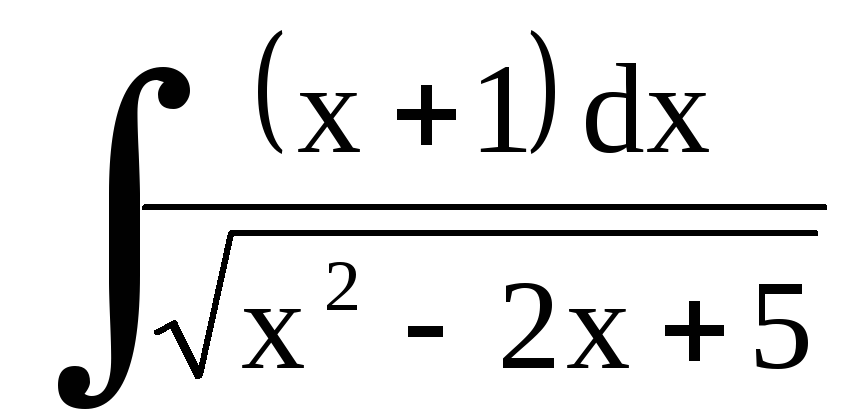7. .	7. .
8. .	8. .
9. .	9. .
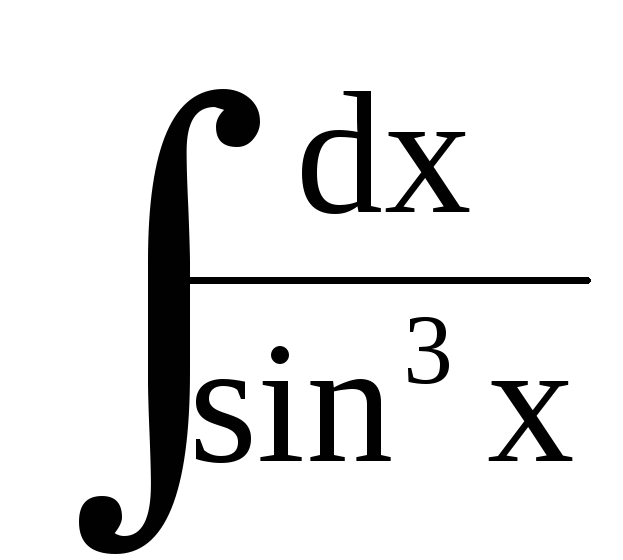