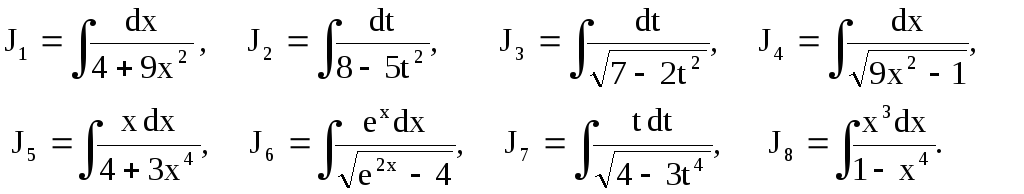Занятие № 1. Интегрирование по формулам

Цель занятия – усвоить и запомнить формулы 1-4 групп, прежде всего формулы (1) - (3) интегралов от степенных функций. Основная формула (1)

, показывает, что при интегрировании степени ее

показатель возрастает на одну единицу. Так, например,

.

Приведем более сложный пример:

.

Здесь воспользовались известным разложением .

Разделив числитель на знаменатель, получим

,

,

,

.

Интеграл можно найти двумя способами. Так как, по свойству 8 приинаходим

.

Другой способ. Полагая здесь , получим

Говорят, что интеграл поправлен на 1/7, иначе говоря, под знак дифференциала подведено основание 7х – 5, чтобы получить точно табличную формулу (1).

Рассмотрим интеграл . Полагая здесь,, получим

. Формулы (2) и (3) суть частные случаи основной формулы (1) при и. Их рекомендуется запомнить, так как они будут часто встречаться в последующем. Приведем примеры.

Так как ,(по свойству 6 неопределенного интеграла),(свойство 8). Аналогично,, поскольку. Во- обще свойства 6 - 8 неопределенного интеграла надо хорошо усвоить. Это позволяет находить простейшие интегралы самым коротким способом. Приведем еще несколько примеров.

, так как здесь .

, так как здесь .

, так как здесь .

, так как здесь .

Теперь обратимся к формуле (4): . Она применяется в тех случаях, когда в числителе стоит дифференциал знаменателя, точнее, когда в числителеможет быть получен дифференциал знаменателя. Приведем примеры.

. Так как , то

,

.

Рассмотрим интеграл от показательной функции и ее частный, но очень важный случай - интеграл от экспоненты:

(свойство 6),

(свойство 8),

Здесь , поэтому

,

. Здесь , поэтому

.

Замечание. Поскольку операция интегрирования является обратной по отноше-нию к операции дифференцирования, полученный ответ всегда можно проверить. Для этого его надо продифференцировать и показать, что получится подынтеграль-ная функция. Так, в последнем примере .

Обратимся к интегрированию гиперболических функций.

Найти интеграл .

Так как , получим

.

Найти интеграл .

Упражнения (устно)

Дайте ответы в следующих примерах.

.

Упражнение

Найти следующие интегралы.

Задание на дом

Занятие № 2. Интегрирование по формулам. Способ подстановки

Цель занятия – усвоить шестую группу формул; овладеть методом замены переменной; научиться брать интегралы, содержащие квадратный трехчлен.

1.К шестой группе формул относятся интегралы функций

где . В каждом примере надо определить, чему равнои, найтии сделать необходимую поправку. Обратите внимание на форму записи.

Примеры.

.

Последний интеграл степенной, так как , если

, поэтому

.

.

Первый интеграл степенной: , где. Второй интеграл также степенной, его можно найти в примере. Поэтому

.

Упражнение. Решить примеры.