
Свойства преобразования Лапласа
Свойства преобразования Лапласа облегчают задачу нахождения изображений для большого числа функций, а также задачу отыскания оригиналов по их изображениям.
Линейность.
Линейной
комбинации оригиналов соответствует
такая же линейная комбинация изображений,
т. е. если
![]()
![]()
![]() и
и![]()
постоянные числа,
то
![]()
Используя свойства интеграла, находим
![]()
![]()
![]()
Пример 3.
Найти изображения функций
![]() – любое число),
– любое число),![]() (соnst).
(соnst).
Решение. Пользуясь свойством линейности и формулой (3), находим

т. е.

Аналогично получаем
формулу
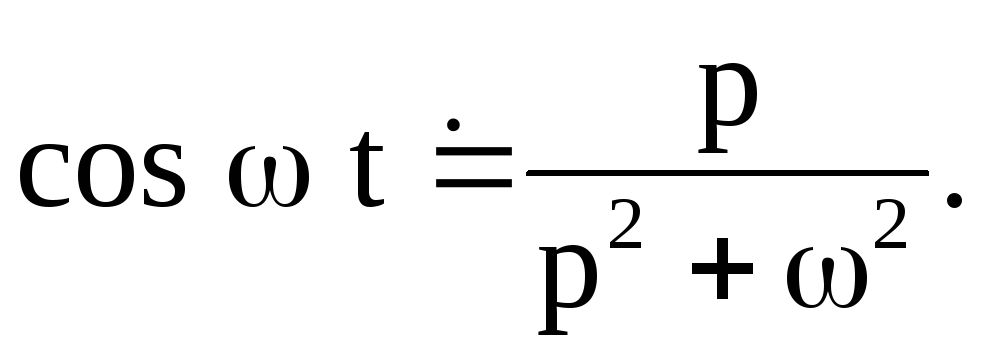
Далее,
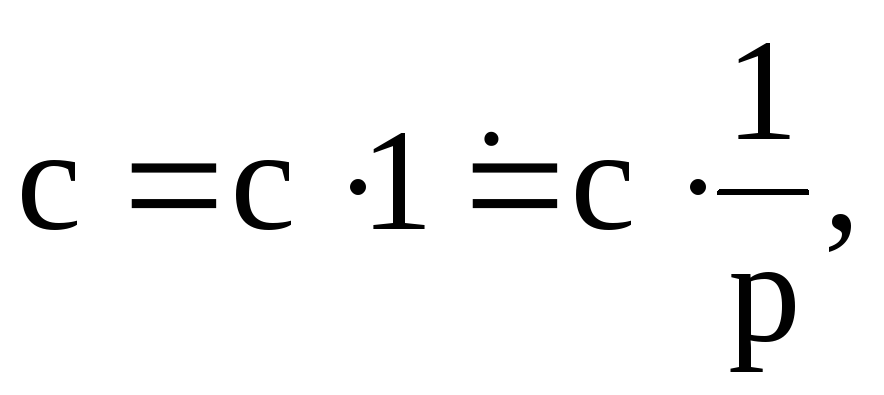 т. е.
т. е.
Подобие
Если
![]() то
то т. е. умножение аргумента
т. е. умножение аргумента
оригинала на
положительное число
![]() приводит к делению изображения и его
аргумента на это число.
приводит к делению изображения и его
аргумента на это число.
По формуле
(1), полагая ![]() получим
получим

![]()
![]()
![]()
(так как безразлично, какой буквой обозначена переменная интегрирования).
Например, пусть

Тогда

![]()
Смещение изображения
Если
![]() то
то![]()
т. е. умножение
оригинала на функцию
![]() влечет за собой смещение переменной
влечет за собой смещение переменной![]()
В силу формулы (1)

![]()
Благодаря этому свойству можно расширить таблицу соответствия между оригиналами и их изображениями:


Запаздывание оригинала
Если
![]() то
то![]() т. е. запаздывание оригинала на
положительную величину
т. е. запаздывание оригинала на
положительную величину![]() приводит к умножению изображения
оригинала без запаздывания на
приводит к умножению изображения
оригинала без запаздывания на![]()
Положив
![]() получим
получим

![]()
Поясним термин
«запаздывание». Графики функции
![]() имеют одинаковый вид, но график функции
имеют одинаковый вид, но график функции![]() сдвинут на
сдвинут на![]() единиц вправо (рис. 3). Следовательно,
функции
единиц вправо (рис. 3). Следовательно,
функции![]() описывают один и тот же процесс, но
процесс, описываемый функцией
описывают один и тот же процесс, но
процесс, описываемый функцией![]() начинается с опозданием на время
начинается с опозданием на время![]()




![]()
![]()
![]()
![]()


t 0 t
Рисунок 3
|
1
0
Рисунок 4 |
Свойство запаздывания удобно применять при отыскании изображения функций, которые на разных участках задаются различными аналитическими выражениями; функций, описывающих импульсные процессы.
|
Функция

![]()
![]() называетсяобобщенной
единичной функцией (рис.
4).
называетсяобобщенной
единичной функцией (рис.
4).
Так как


Пример 4.
Найти
изображение функции

![]()

|
Решение. Данная
функция описывает единичный импульс
(рис. 5), который можно рассматривать
как разность оригиналов единичной
функции
|
1
0 3 t
Рисунок 5 |
Дифференцирование оригинала
Если
![]() и функции
и функции![]() являются оригиналами, то
являются оригиналами, то
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]()
![]() (7)
(7)
По определению
изображения

Возьмем интеграл
по частям, полагая ![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
Тогда

![]()
![]()
Итак,
![]() Пользуясь полученным результатом,
найдем изображение второй производной:
Пользуясь полученным результатом,
найдем изображение второй производной:
![]()
Аналогично найдем изображение третьей производной:
![]()
Применяя формулу
(4)
![]() раз, получим формулу (7).
раз, получим формулу (7).
Замечание.
Формулы (4) – (7) просто выглядят при
нулевых начальных условиях: если
![]() то
то![]() если
если![]() то
то
![]() и, наконец, если
и, наконец, если
![]() то
то
![]() т. е. дифференцированию
оригинала соответствует умножение его
изображения на p.
т. е. дифференцированию
оригинала соответствует умножение его
изображения на p.
Свойство дифференцирования оригинала вместе со свойством линейности широко используется при решении линейных дифференциальных уравнений.
Дифференцирование изображения
Если
![]() то
то
![]()
![]()
![]() ,
,
![]()
![]()
т. е. дифференцированию
изображения соответствует умножение
его оригинала на
![]()
Согласно теореме
1 существования изображения,
![]() является аналитической функцией в
полуплоскости
является аналитической функцией в
полуплоскости![]() Следовательно, у нее существует
производная любого порядка. Дифференцируя
интеграл (1) по параметруp
получим
Следовательно, у нее существует
производная любого порядка. Дифференцируя
интеграл (1) по параметруp
получим
![]()
![]()
т. е.
![]()
Тогда
![]()
![]() и вообще
и вообще
![]()
Пример 5. Найти
изображения функций
![]()
Решение. Так
как
 по свойству дифференцирования
изображения
по свойству дифференцирования
изображения
имеем

Далее находим
 т. е.
т. е.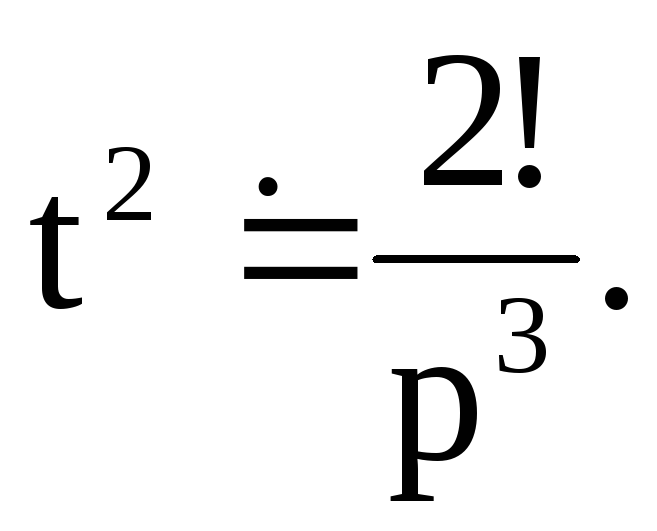
Продолжая
дифференцирование, получим
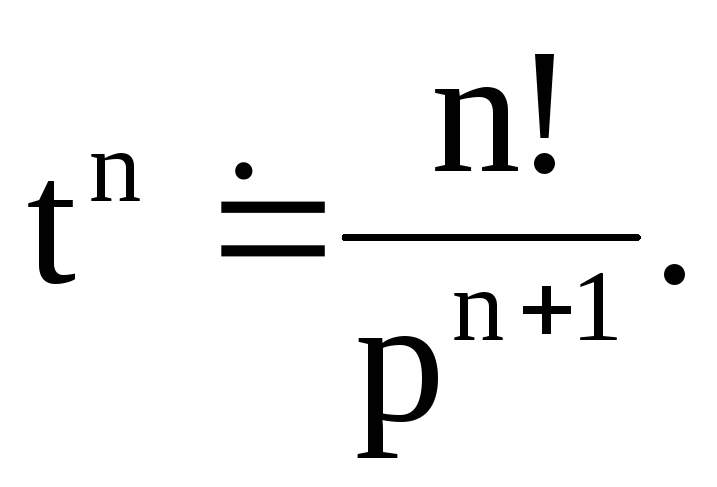
Так как


т. е.
 или
или
Аналогично
находим

Интегрирование оригинала
Если
![]() то
то![]() т. е. интегрирование оригинала от
т. е. интегрирование оригинала от![]() до
до![]() соответствует делению его изображения
на
соответствует делению его изображения
на![]() .
.
Функция
![]() является оригиналом (проверьте
самостоятельно).
является оригиналом (проверьте
самостоятельно).
Пусть
![]() Тогда по свойству дифференцирования
оригинала
Тогда по свойству дифференцирования
оригинала
![]()
(![]() ).
).
А так как

![]()
Отсюда
![]()
![]() т. е.
т. е.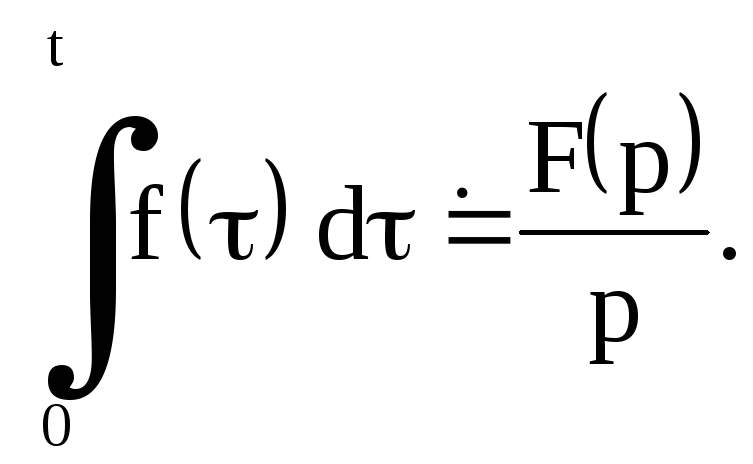
Интегрирование изображения
Если
![]() и интеграл
и интеграл![]() сходится, то
сходится, то
т. е. интегрирование
изображения от
![]() соответствует делению его оригинала
наt.
соответствует делению его оригинала
наt.
Используя формулу (1) и изменяя порядок интегрирования, получаем
![]()

Пример 6. Найти
изображения функции
![]() и интегрального синуса
и интегрального синуса![]()
Решение.
Так как
 функция
функция
 т. е.
т. е.
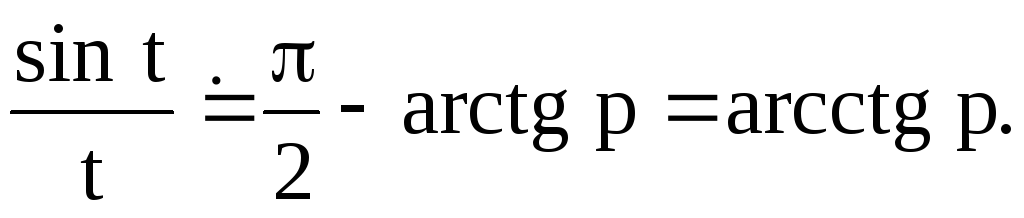
Применяя свойство интегрирования оригинала, получаем

Умножение изображений
Если
![]()
![]() то
то
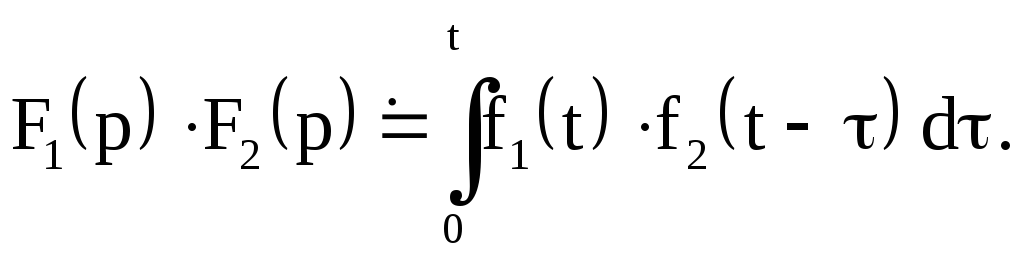
Интеграл в правой
части формулы называется сверткой
функций
![]() и обозначается
символом
и обозначается
символом
![]() т. е.
т. е.
![]()
Можно убедиться
(положив
![]() ),
что свертывание обладает свойством
коммутативности, т. е.
),
что свертывание обладает свойством
коммутативности, т. е.
![]() =
=![]() .
.
Итак, умножение изображений соответствует свертке их оригиналов
![]()
![]() .
.
Пример 7.
Найти оригинал функции
![]()
Решение. Так
как
![]() и
и

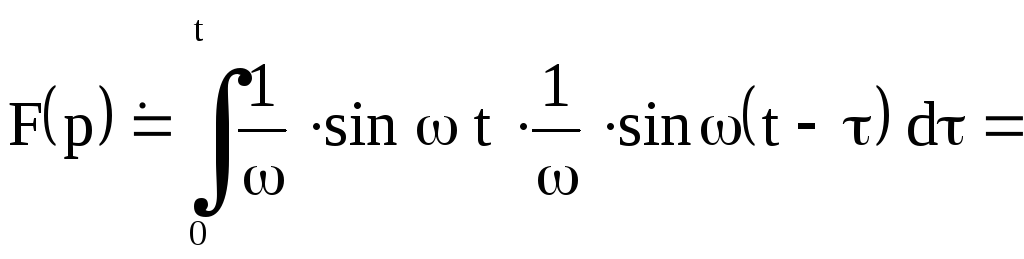
![]()
![]()
![]()
т.е.

Следствие.
Если
![]() также является оригиналом, то
также является оригиналом, то
 (8)
(8)
Запишем
произведение
![]() в виде
в виде
![]()
или
![]()
Первое слагаемое
в правой части есть произведение
изображений, соответствущих оригиналам
 и
и![]() Поэтому на основании свойства умножения
изображений и линейности можно записать
Поэтому на основании свойства умножения
изображений и линейности можно записать
![]()
![]()
или

Формула (8) называется формулой Дюамеля.
На основании свойства коммутативности свертки формулу Дюамеля можно записать в виде

Формулу Дюамеля можно применять для определения оригиналов по известным изображениям.
Пример 8. Найти оригинал, соответствующий изображению
![]()
Решение: Так как
![]() и
и

на основании формулы Дюамеля (8)

Умножение оригиналов
|
Если
где
путь интегрирования – вертикальная
прямая
|
0 s
Рисунок 6
|
Изображение периодического оригинала с периодом, равным T, имеет вид
![]()
Оно определено в
полуплоскости
![]()
Пример 9.
Найти
изображение периодической функции
![]() заданной графически (рис. 7).
заданной графически (рис. 7).
|
|
1
0 1 2 3 4 t
Рисунок 7 |
Решение.
Зададим
![]() аналитически
аналитически

![]()
![]()
учтем, что
![]() ,
получим
,
получим

Кратко перечислим рассмотренные свойства преобразования Лапласа
1. Линейность:
![]()
2.Подобие:
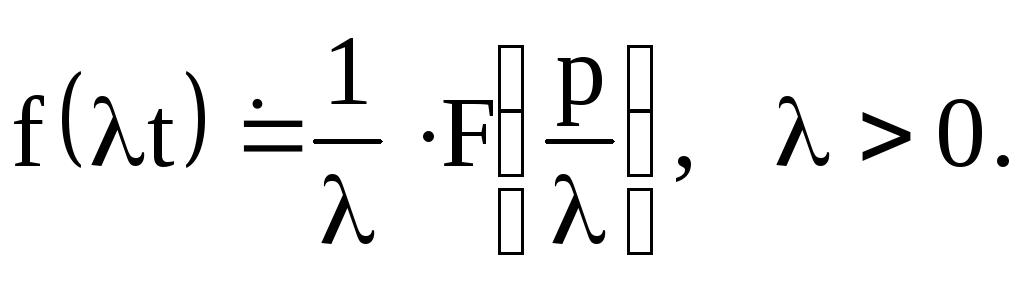
3. Смещение:
![]()
4. Запаздывание:
![]()
5. Дифференцирование оригинала:
![]()
![]()
![]()
![]()
Дифференцирование изображения

7. Интегрирование
оригинала:

Интегрирование изображения:

Умножение изображений:

Умножение оригиналов:

Приведем таблицу часто встречающихся оригиналов и их изображений:
|
|
Оригинал
|
Изображение
|
|
1. |
1 |
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
6. |
|
|
|
7. |
|
|
|
8. |
|
|
|
|
Оригинал
|
Изображение
|
|
9. |
|
|
|
10.
|
|
|
|
11. |
|
|
|
12. |
|
|
|
13. |
|
|
|
14. |
|
|
|
15. |
|
|
|
16. |
|
|
|
17. |
|
|
|
18. |
|
|
|
19. |
|
|
|
20. |
|
|
|
21.
|
|
|
|
22. |
|
|
|
23. |
|
|


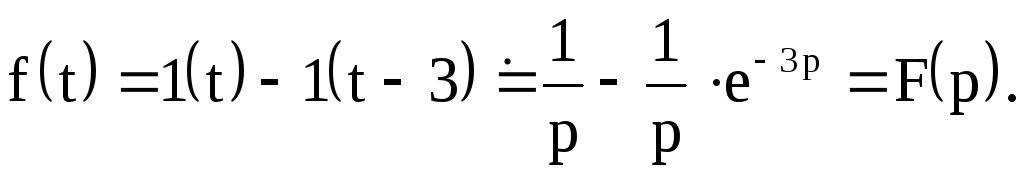


 то
то


