
Операционное исчисление – это один из методов математического анализа, позволяющий в ряде случаев свести решение дифференциальных и некоторых типов интегральных уравнений к решению более простых алгебраических задач.
Операционное исчисление играет важную роль при решении прикладных
задач, что особенно важно для студентов технического вуза.
С помощью операционного исчисления можно также находить решения линейных дифференциальных уравнений с переменными коэффициентами, уравнений в частных производных, уравнений в конечных разностях (разностных уравнений); производить суммирование рядов; вычислять интегралы. При этом решение этих и других задач значительно упрощается.
Оригиналы и их изображения
Основными понятиями операционного исчисления являются понятия функции-оригинала и функции-изображения.
Пусть
![]() – действительная функция действительного
переменного
– действительная функция действительного
переменного![]() (под
(под![]() будем понимать время или координату).
будем понимать время или координату).
Функция
![]() называетсяоригиналом,
если она
удовлетворяет следующим условиям:
называетсяоригиналом,
если она
удовлетворяет следующим условиям:
1.
![]() при
при![]()
2.
![]() – кусочно-непрерывная при
– кусочно-непрерывная при![]() т. е. она непрерывна или имеет точки
разрыва 1-го рода, причем на каждом
конечном промежутке оси
т. е. она непрерывна или имеет точки
разрыва 1-го рода, причем на каждом
конечном промежутке оси![]() таких точек только конечное число,
причем
таких точек только конечное число,
причем![]()
3. Существуют
такие числа
![]() что для всех
что для всех![]() выполняется неравенство
выполняется неравенство![]() ,
т. е. при возрастании
,
т. е. при возрастании![]() функция
функция![]() может возрастать не быстрее некоторой
показательной функции. Число
может возрастать не быстрее некоторой
показательной функции. Число![]() (точная нижняя граница такихs)
называется
показателем
роста
(точная нижняя граница такихs)
называется
показателем
роста
![]() .
.
Первое условие
означает, что процесс начинается с
некоторого момента времени; удобнее
считать, что в момент
![]() Третьему условию удовлетворяют
ограниченные функции
Третьему условию удовлетворяют
ограниченные функции![]() степенные
степенные![]() и многие другие.
и многие другие.
Не являются
оригиналами, например, функции вида
![]() (не выполняется
условие 3), функции
(не выполняется
условие 3), функции
![]() (не выполняется условие 2).
(не выполняется условие 2).
Условия 1) – 3) выполняются для большинства функций, описывающих различные физические процессы.
Замечание.
Функция
![]() может быть и комплексной функцией
действительного переменного, т. е. иметь
вид
может быть и комплексной функцией
действительного переменного, т. е. иметь
вид![]() она считается оригиналом, если
действительные функции
она считается оригиналом, если
действительные функции![]() и
и![]() являются
оригиналами.
являются
оригиналами.
Изображением
оригинала
![]() называется функция
называется функция![]() комплексного переменного
комплексного переменного![]() ,
определяемая интегралом
,
определяемая интегралом
![]() (1)
(1)
Операцию перехода
от оригинала
![]() к изображению
к изображению![]() называютпреобразованием
Лапласа.
Соответствие между оригиналом
называютпреобразованием
Лапласа.
Соответствие между оригиналом
![]() и изображением
и изображением![]() записывается в виде
записывается в виде![]() или
или![]() ,
а также
,
а также![]() (принято оригиналы обозначать малыми
буквами, а их изображения – соответствующими
большими буквами).
(принято оригиналы обозначать малыми
буквами, а их изображения – соответствующими
большими буквами).
Теорема 1
(существование изображения).
Для всякого оригинала
![]() изображение
изображение![]() существует в полуплоскости
существует в полуплоскости![]() где
где![]() показатель роста функции
показатель роста функции![]() ,
причем функция
,
причем функция![]() является аналитической в этой
полуплоскости
является аналитической в этой
полуплоскости![]()
|
Рисунок 1 |
Докажем
первую часть теоремы. Пусть
|
![]()
![]()
так как
![]()
Таким образом,
![]() (2)
(2)
Отсюда вытекает
абсолютная сходимость интеграла (1), т.
е. изображение
![]() существует и однозначно в полуплоскости
существует и однозначно в полуплоскости![]()
Следствие
(необходимый признак существования
изображения).
Если функция
![]() является изображением функции
является изображением функции![]() ,
то
,
то
![]()
Это утверждение
непосредственно вытекает из неравенства
(2), когда
![]()
Так как
![]() – аналитическая функция в полуплоскости
– аналитическая функция в полуплоскости![]() то
то![]() при
при![]() по любому направлению. Отсюда, в
частности, следует, что функции
по любому направлению. Отсюда, в
частности, следует, что функции![]()
![]() не могут
быть изображениями.
не могут
быть изображениями.
Отметим, что из
аналитичности функции
![]() следует, что все ее особые точки должны
лежать левее прямой
следует, что все ее особые точки должны
лежать левее прямой![]() или на самой этой прямой. Функция
или на самой этой прямой. Функция![]() ,
не удовлетворяющая этому условию, не
является изображением функции
,
не удовлетворяющая этому условию, не
является изображением функции![]() .
Не является изображением, например,
функция
.
Не является изображением, например,
функция![]() (ее особые точки расположены на всей
осиs).
(ее особые точки расположены на всей
осиs).
Теорема 2 (о
единственности оригинала). Если
функция
![]() служит изображением двух оригиналов
служит изображением двух оригиналов![]() то эти оригиналы совпадают друг с другом
в тех точках, в которых они непрерывны.
то эти оригиналы совпадают друг с другом
в тех точках, в которых они непрерывны.
|
Пример 1. Найти изображение единичной функции Хевисайда
(рис. 2). |
Рисунок 2 |
Решение.
По формуле (1) при
![]() находим
находим
![]()

т. е.
![]() или, в символической записи,
или, в символической записи, или
или 
Замечание. В
дальнейшем функцию-оригинал будем
кратко записывать в виде
![]() подразумевая, что
подразумевая, что

![]()
![]()
Пример 2. Найти
изображение функции
![]() где
где![]() любое число.
любое число.
Решение. Данная функция является оригиналом. По формуле (1) имеем

![]()
если
![]()
Таким образом,
 (3)
(3)




 0
s0
s
0
s0
s
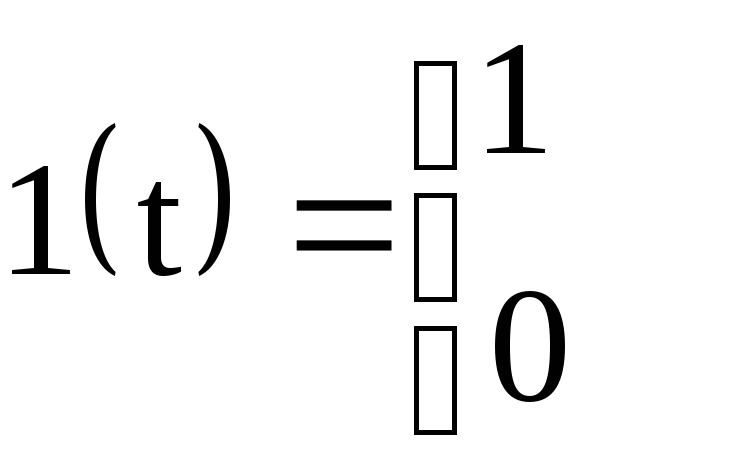
 1(t)
1(t) 1
1

