Задачи для решения в аудитории

1. Совместное распределение случайных величин задано таблицей

Величины -1 0 1 -1 1

Найти ряды распределения для и. Будут ли независимыи?

2. По цели производятся два независимых выстрела. Вероятность попадания в цель при первом выстреле равна , при втором –. Построить таблицу распределения системы двух случайных величин, где- число попаданий при первом выстреле,- число попаданий при втором выстреле. Найти функцию распределения системы.

3. Независимые случайные величины иподчинены следующим законам распределения:,

Написать выражение функции распределения системы двух случайных величин .

4. Дана функция распределения системы двух случайных величин :

Определить, зависимы ли случайные величины . Найти плотность распределения вероятностей системы. Вычислить числовые характеристики.

5. Система случайных величин имеет плотность

.

Определить величину . Найти функцию распределения,,. Определить вероятность попадания случайной точкив область, заданную неравенствами:.

6. Система двух случайных величин , подчинена закону равномерной плотности внутри прямоугольника:. Найти плотность распределения вероятности и вероятностьпопадания случайной точкив квадрат со стороной, если центр этого квадрата совпадает с началом координат.

7. Плотность распределения вероятностей систем двух независимых случайных величин задана следующим выражением:

.

Найти неизвестный параметр и определить корреляционную матрицу системы.

Задачи для решения в аудитории

8. Закон распределения системы двух случайных величин задан таблицей распределения (рис. 1). Найти следующие характеристики системы:.

Величины	0	1
-1	0,10	0,15
0	0,15	0,25
1	0,20	0,15

Рисунок 6

9. Случайные величины независимы и их плотности распределения вероятностей соответственно равны:

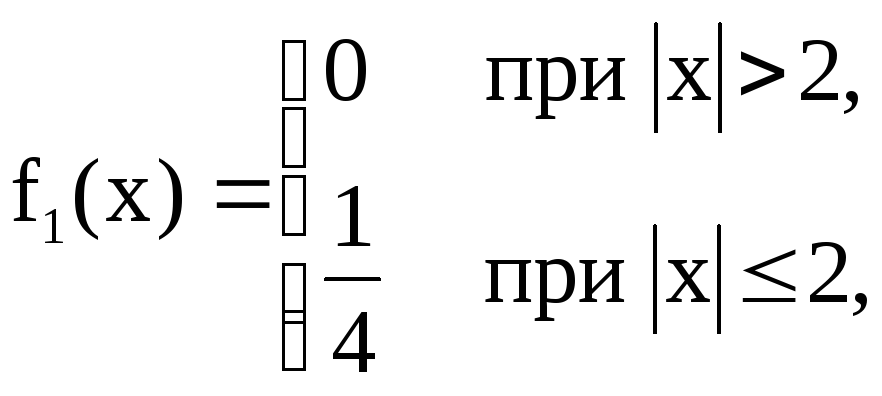
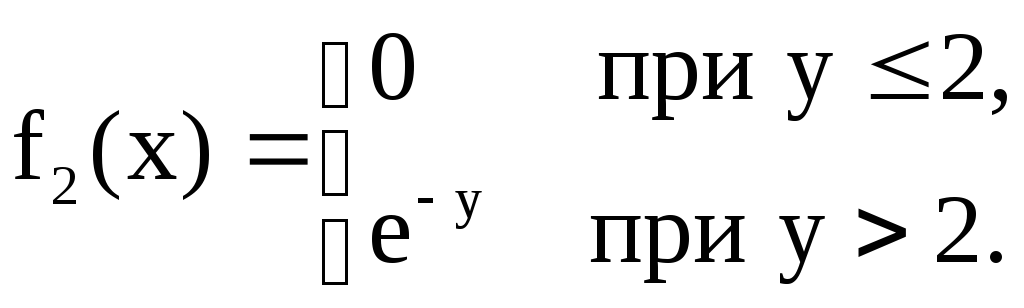
Определить функцию распределения системы случайных величин . Найти числовые характеристики системы случайных величин.

10. Функция совместного распределения случайных величин задана выражением

Определить, зависимы ли случайные величины . Найти плотность распределения вероятностей системы. Найти вероятность одновременного выполнения неравенств.

11. Определить математическое ожидание и корреляционную матрицу системы двух случайных величин , если плотность распределения вероятностей системы имеет следующий вид:

.

Определить вероятность попадания случайной точки в круг радиусом.

12. Случайная точка имеет равномерное распределение внутри прямоугольника, ограниченного прямыми. Найти функцию распределениясистемы случайных величин.

13. Система двух случайных величин имеет плотность распределения вероятностей.

Найти следующие числовые характеристики системы

.