
Задачи для самостоятельного решения
4.9.
Разложить в ряд Лорана по степеням
![]() функцию
функцию![]() в окрестности точки
в окрестности точки![]() .
.
4.10.
Разложить в ряд Лорана по степеням
![]() функцию
функцию![]() в окрестности точки
в окрестности точки![]() .
.
4.11.
Разложить в ряд Лорана
![]() функцию
функцию по степеням
по степеням![]() в области
в области![]() .
.
4.12.
Разложить в ряд Тейлора или Лорана
функцию
![]() в окрестности точек: а)
в окрестности точек: а)![]() ;
б)
;
б)![]() .
.
4.13. Найти порядки нулей функций:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
4.14.
Определить характер точек
![]() следующих функций:
следующих функций:
|
а)
|
б)
|
|
в)
|
г)
|
|
д)
| |
4.15.
Найти особые точки функций, выяснить
их характер и исследовать поведение
функций на бесконечности: а)
![]() б)
б)![]() .
.
ВЫЧЕТЫ И ИХ ПРИЛОЖЕНИЯ
Вычетом
функции
![]() относительно конечной изолированной
особой точки
относительно конечной изолированной
особой точки![]() называется число, обозначаемое
называется число, обозначаемое![]() и определяемое равенством
и определяемое равенством ,
где
,
где
![]() – любая окружность с центром
– любая окружность с центром![]() ,
внутри которой
,
внутри которой![]() – единственная особая точка;
– единственная особая точка;![]() .
Здесь
.
Здесь![]() – коэффициент при
– коэффициент при![]() в разложении
в разложении![]() в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки![]() .
.
Если
![]() – устранимая особая точка
– устранимая особая точка![]() ,
то
,
то![]() .
.
Если
![]() – простой полюс
– простой полюс![]() ,
то
,
то![]() .
.
Если
 ,
где
,
где![]() и
и ![]() аналитичны в точке
аналитичны в точке
![]() ,
,
![]() (т.
е.
(т.
е.
![]() – простой полюс
– простой полюс![]() ),
то
),
то
 .
.
Если
![]() – полюс
– полюс![]() -го
порядка для
-го
порядка для
![]() ,
то
,
то
 .
.
Пример 22.
Определить вычеты функции
 относительно точек
относительно точек![]() .
.
Решение.

 .
.

или

 .
.
Пример 23.
Определить вычет функции
![]() относительно особой точки
относительно особой точки![]() .
.
Решение.
Точка
![]() – существенно особая точка (см. пример
20).
– существенно особая точка (см. пример
20).
Ряд Лорана для
функции
![]() в области
в области![]() имеет вид
имеет вид
 ;
;
![]() .
.
Основная теорема
о вычетах.
Если функция
![]() аналитична на простом замкнутом контуре
аналитична на простом замкнутом контуре![]() и внутри него, за исключением конечного
числа особых точек
и внутри него, за исключением конечного
числа особых точек![]() ,
лежащих внутри
,
лежащих внутри![]() ,
то
,
то
 .
.
Пример 24.
Вычислить
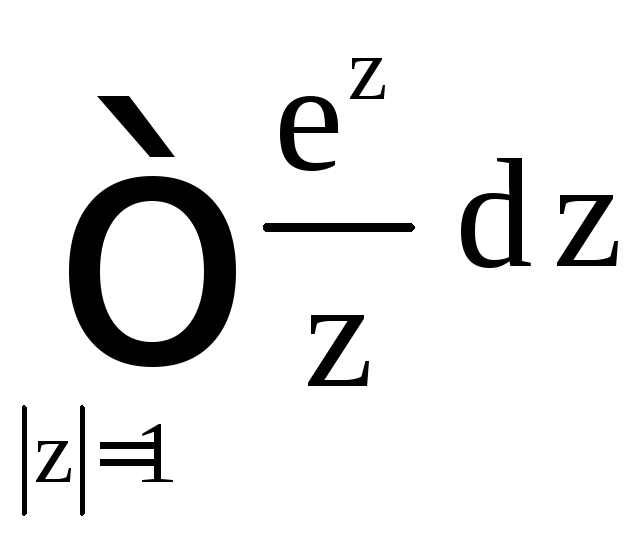 .
.
Решение. Функция
![]() имеет одну особую
изолированную точку
имеет одну особую
изолированную точку
![]() (полюс 1-го порядка), лежащую в области
(полюс 1-го порядка), лежащую в области![]() .
Значит,
.
Значит,
 .
.
Пример 25.
Вычислить
 ,
где
,
где![]() – окружность
– окружность![]() .
.
Решение.
 .
.
![]() –полюс 3-го порядка,
–полюс 3-го порядка,
![]() – полюсы 1-го порядка, лежащие внутри
контура интегрирования, тогда
– полюсы 1-го порядка, лежащие внутри
контура интегрирования, тогда
 ;
;

 ;
;
![]() ;
;
![]() .
.
 .
.
Пример 26. Вычислить
 .
.
Решение.
![]() – существенно особая точка, т. к.
– существенно особая точка, т. к.![]() не существует.
не существует.
 ;
;
 ;
;
 ;
;
 .
.
Вычетом
относительно бесконечно
удаленной
изолированной особой точки функции
![]() называется обозначаемое
называется обозначаемое![]() число, равное
число, равное
 ,
,
где
![]() – любая окружность с центром в точке
– любая окружность с центром в точке![]() ,
содержащая внутри себя все особые точки
,
содержащая внутри себя все особые точки![]() ,
кроме точки
,
кроме точки![]() ,
и контур
,
и контур![]() обходится по часовой стрелке
обходится по часовой стрелке![]() ,
где
,
где
![]() – коэффициент при
– коэффициент при![]() в разложении
в разложении
![]() в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки![]() .
.
Если функция
![]() аналитична в расширенной комплексной
плоскости всюду, за исключением конечного
числа особых точек, то сумма вычетов
функции
аналитична в расширенной комплексной
плоскости всюду, за исключением конечного
числа особых точек, то сумма вычетов
функции![]() относительно всех ее особых точек равна
нулю.
относительно всех ее особых точек равна
нулю.
Пусть функция
![]() есть функция аналитическая всюду в
верхней полуплоскости, включая
действительную ось, за исключением
конечного числа особых точек
есть функция аналитическая всюду в
верхней полуплоскости, включая
действительную ось, за исключением
конечного числа особых точек
![]() ,
лежащих в верхней полуплоскости. Кроме
того, бесконечно удаленная точка есть
нуль не ниже второго порядка для функции
,
лежащих в верхней полуплоскости. Кроме
того, бесконечно удаленная точка есть
нуль не ниже второго порядка для функции
![]() ,
т. е.
,
т. е.![]() .
Тогда
.
Тогда
 .
.
Пример 27. Вычислить
интеграл
 .
.
Решение.
 удовлетворяет
всем условиям сформулированной теоремы.
удовлетворяет
всем условиям сформулированной теоремы.
![]() –простые полюсы,
лежащие в верхней полуплоскости.
–простые полюсы,
лежащие в верхней полуплоскости.
Тогда

 .
.
Если функция
![]() ,
причем
,
причем![]() аналитична всюду в верхней полуплоскости,
включая действительную ось, за исключением
конечного числа особых точек
аналитична всюду в верхней полуплоскости,
включая действительную ось, за исключением
конечного числа особых точек![]() ,
лежащих в верхней полуплоскости, кроме
того, бесконечно удаленная точка является
нулем функции
,
лежащих в верхней полуплоскости, кроме
того, бесконечно удаленная точка является
нулем функции![]() ,
т. е.
,
т. е.
![]() ,
то
,
то
 .
.
Пример 28. Вычислить
интеграл
 .
.
Решение
 ,
т. к. подынтегральная функция четная.
,
т. к. подынтегральная функция четная.
 .
.
Функция ![]() удовлетворяет
условиям сформулированной выше теоремы.
удовлетворяет
условиям сформулированной выше теоремы.
![]() – полюс 1-го порядка, лежащий в верхней
полуплоскости. Тогда
– полюс 1-го порядка, лежащий в верхней
полуплоскости. Тогда
 ;
;

 .
.
Задачи
5.1. Вычислить вычеты следующих функций относительно их конечных особых точек:
|
а)
|
б)
|
в)
|
г)
|
д)
|
5.2. Вычислить с помощью вычетов следующие интегралы:
|
а)
|
б)
|
|
в)
|
г)
|
5.3. Вычислить с помощью вычетов следующие несобственные интегралы:
|
а)
|
б)
|
в)
|


 ,
, ,
, ,
,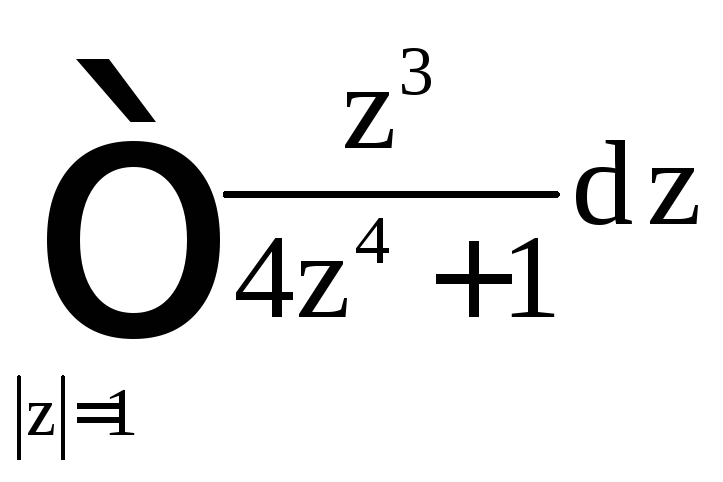 ,
, ,
, ,
где
,
где ;
; ;
; .
.