Задачи для самостоятельного решения

3.14. Вычислить , где– отрезок прямой, соединяющей точ- кии.

3.15. Вычислить , где– прямолинейный отрезок, соединяющий точки.

3.16. Вычислить , где– ломаная линияс вершинами в точках.

3.17. Вычислить по следующим линиям: а)– отрезок действительной оси от точкидо точки; б)– полуокружность.

3.18. Вычислить .

3.19. Вычислить по произвольной линии, соединяющей точки.

3.20. Какие значения может иметь интеграл , если за пути интегрирования принимать любые пути, вдоль которых подынтегральная функция непрерывна?

3.21. Вычислить , где.

3.22. Вычислить .

3.23. Вычислить , где– эллипс.

3.24. Вычислить , где– эллипс

3.25. Вычислить , если

а) точка 0 лежит внутри, а точка 1 – вне контура ;

б) точка 1 лежит внутри, а точка 0 – вне контура ;

в) обе точки 0 и 1 лежат внутри контура .

РЯДЫ ТЕЙЛОРА И ЛОРАНА

Если – аналитическая функция в круге, то она разлагается в этом круге вряд Тейлора:

или ,

где .

(– любая окружность с центром, лежащая внутри круга).

Если – аналитическая функция внутри кольца,, то она разлагается в этом кольце вряд Лорана:

или ,

где

(– любая окружность с центром, лежащая внутри кольца).

Ряд называется главной частью ряда Лорана, а ряд называется правильной частью ряда Лорана.

Разложения в ряд Тейлора и Лорана единственны.

Пример 15. Написать разложение функции по степенямв областив ряд Тейлора или Лорана:

а)	б)
в)

Решение. а) Степенной ряд функции в области является рядом Лорана, т. к. рассматриваемая область аналитичности этой функции есть кольцо .

Представим функцию в виде.

В окрестности точки выполняется неравенство, поэтому дробьможно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом и знаменателем.

.

б) Степенной ряд функции в области является рядом Тейлора, т. к. рассматриваемая область аналитичности функции есть круг.

Определим коэффициенты ряда Тейлора:

Ряд Тейлора для функции в области будет иметь вид

в) Степенной ряд функции в областиявляется рядом Лорана, т. к. рассматриваемая область аналитичности этой функции есть кольцо: .

Разложим функцию на простейшие дроби:

приняв во внимание, что при , можем записать

Следовательно,

где .

Пример 16. Разложить в ряд Лорана или Тейлора функцию

в окрестности точек а) б)

Решение. а) В окрестности точки данная функция разлагается в ряд Тейлора:

.

Последняя дробь есть сумма членов бесконечно убывающей геометрической прогрессии в области , т. е.

б) В окрестности точки функция разлагается в ряд Лорана. Функция уже представлена в виде отрицательной степени. Так как разложение в ряд Лорана единственно, есть разложение функции в ряд Лорана.

Если , то точканазываетсянулем функции. Если в разложении функции в ряд Тейлора в окрестности точки

и, следовательно, ряд Тейлора имеет вид

,

то точка называетсянулем функции -го порядка или -й кратности.

Из определения следует, что если точка – нуль-го порядка, то

Для того чтобы точка была нулем функции -го порядка, необходимо и достаточно, чтобы в окрестности точкиимело место равенство

,

где – аналитическая функция в точке.

Пример 17. Определить нули функции и их порядок.

Решение. – нули 1-го порядка, т. к.

.

Пример 18. Определить нули функции и их порядок.

Решение. – нули 1-го порядка;– нули 2-го порядка. Точка, в которой нарушается аналитичность функции, является для этой функцииособой точкой. Особая точка называетсяизолированной особой точкой функции , если существует окрестность, в которой функция аналитична.

Если разложение функции в окрестности изолированной особой точкив ряд Лорана

1) не содержит отрицательных степеней , то точканазываетсяустранимой особой точкой;

2) содержит конечное число членов с отрицательными степенями , то точканазываетсяполюсом функции ;

3) содержит бесчисленное множество членов с отрицательными степенями , то точканазываетсясущественно особой точкой функции .

Для того чтобы изолированная особая точка была устранимой особой точкой, полюсом или существенно особой точкой функции, необходимо и достаточно, чтобы при стремлениикфункцияимела соответственно конечный предел, бесконечный предел или не имела предела (ни конечного, ни бесконечного).

Если – устранимая особая точка, то после доопределения функциив этой точке по непрерывностифункция становится аналитичной в точке.

Если – полюс, то в окрестности точки

,

где .

Число называетсяпорядком полюса. Полюс 1-го порядка называется простым полюсом.

Для того чтобы точка была полюсом-го порядка, необходимо и достаточно, чтобы в окрестности точкиимело место равенство

,

где – аналитическая функция в точке.

Если функция аналитична в окрестностибесконечно удаленной точки, то точка называетсяизолированной особой точкой . При этом точканазывается устранимой особой точкой функции, полюсом или существенно особой точкой, если разложениев ряд Лорана в окрестности точки

соответственно не содержит положительных степеней , содержит конечное число положительных степенейили содержит бесконечное множество положительных степеней.

Подстановка сводит изучение функции в окрестности точкик изучению функции в окрестности точки.

Пример 19. Определить характер точки для функции.

Решение. – особая точка функции. Для выяснения ее характера

разложим функцию в ряд Лорана в области .

Так как разложение не содержит отрицательных степеней , то точка– устранимая особая точка.

Пример 20. Найти особые точки функции и выяснить их характер.

Решение. Точка – особая точка. Для выяснения ее характера разложим функциюв ряд Лорана в области.

;

;

.

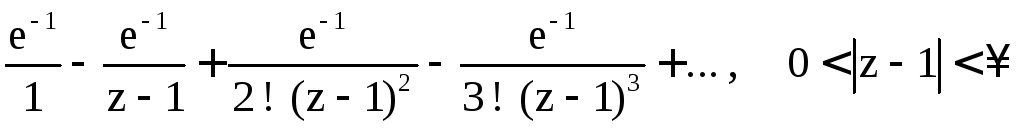–существенно особая точка.

Выясним характер особой точки . Для этого, положив, получим, причем точкадля этой функции является правильной.

Разложим функцию в областив ряд Тейлора:

Отсюда

т. е.

Следовательно, точка – устранимая особая точка.

Если – устранимая особая точка функции, то говорят, что она аналитична в бесконечности и принимают.

Если функция аналитична в бесконечно удаленной точке и, то точканазывается нулем-го порядка функции, если

.

Пример 21. Найти особые точки функции , выяснить их характер и исследовать поведение функции на бесконечности.

Решение. .

–полюс 3-го порядка; – полюсы 2-го порядка;– нуль 7-го порядка.

Задачи

4.1. Разложить в ряд Тейлора функцию по степенямв окрестности точки.

4.2. Написать разложение функции по степенямв областив ряд Лорана или Тейлора: а); б); в).

4.3. Разложить в ряд Тейлора или Лорана функцию в окрестности точек: а); б); в).

4.4. Зная разложение , найти разложение по степенямфункциипри.

4.5. Разложить в ряд Лорана функцию в кольцеи в окрестности точки (в последнем случае надлежит определить окрестность, в которой разложение имеет место).

4.6. Найти порядки нулей данных функций:

а) ; б); в); г).

4.7. Определить характер точек следующих функций:

а)

б)

в)

г)

д)

е)

4.8. Найти особые точки функций, выяснить их характер и исследовать поведение функций на бесконечности: а) б)