§6. Дискретные случайные величины. Непрерывные случайные величины. Числовые характеристики случайных величин

Случайная величина называется дискретной, если ее возможные значения можно перенумеровать. Дискретная случайная величина может быть задана рядом распределения или функцией распределения. Рядом распределения называется совокупность всех возможных значений и соответствующих им вероятностей

			…
			…

.

Функцией распределения случайной величины Х называется функция , равная вероятноститого, что случайная величина будет меньше произвольно выбранного значениях. Функция вычисляется по формуле

,

где суммирование ведется по всем значениям i, для которых .

Случайная величина называется непрерывной, если существует неотрицательная функция , удовлетворяющая при всех х равенству

.

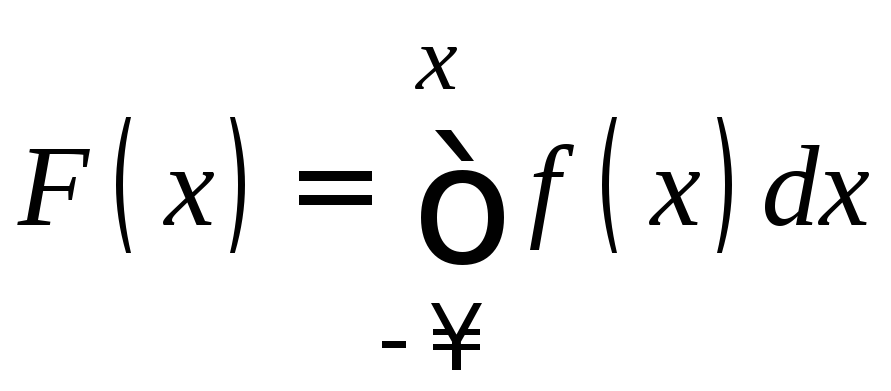Функция называетсяплотностью распределения

.

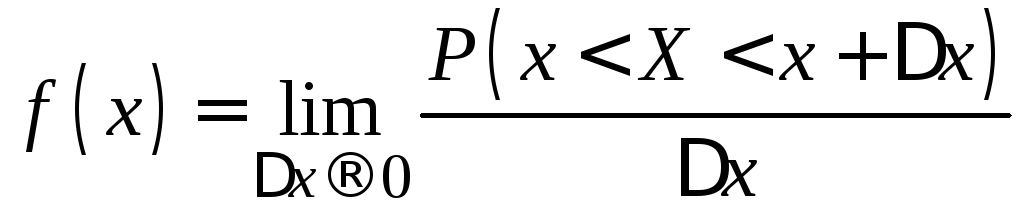Непрерывная случайная величина задается либо функцией распределения либо плотностью распределения. Функция распределения , гдех – произвольное действительное число, дает вероятность того, что случайная величина Х окажется меньше х.

Функция имеет следующие основные свойства:

1.

2.

3.

4.

Плотность распределения обладает следующими основными свойствами:

1. ,

2. ,

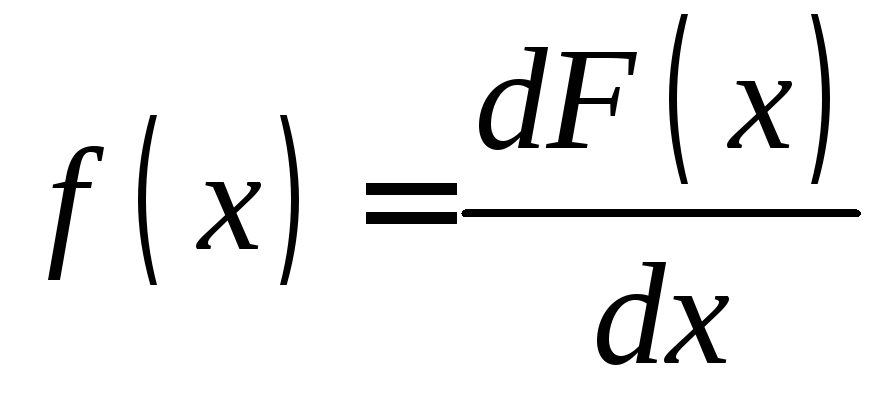3. ,

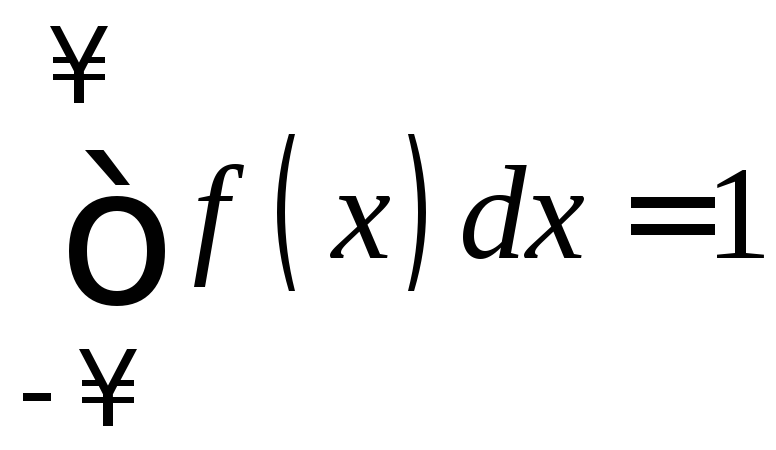4. .

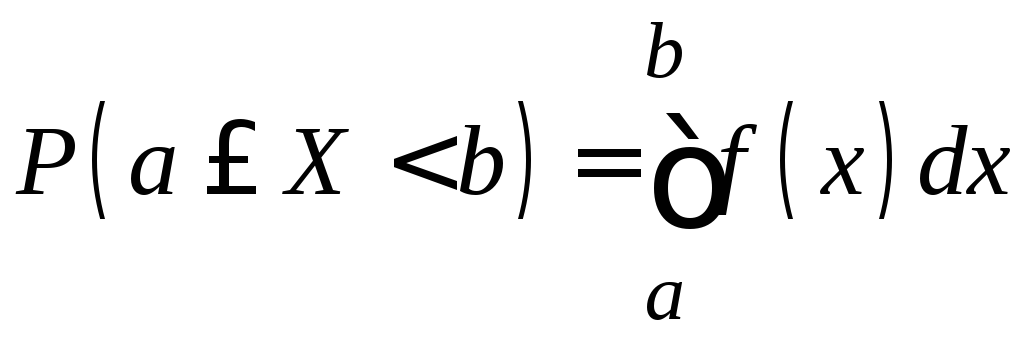Пусть дискретная случайная величина принимает значения с вероятностямисоответственно, тогдаматематическим ожиданием или средним значением случайной величины называется число

.

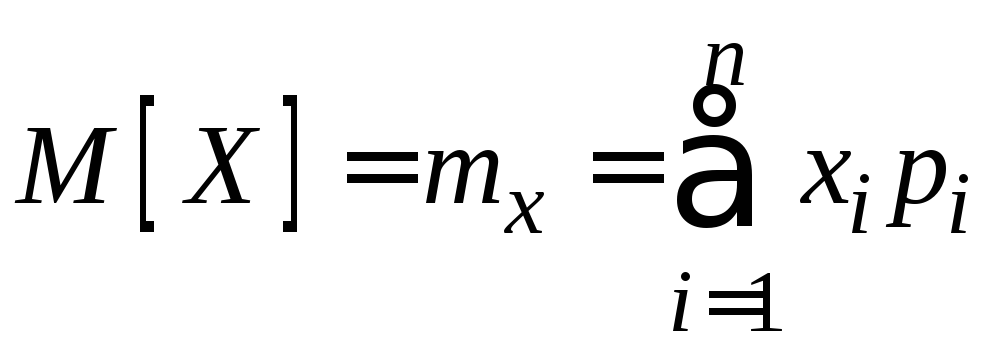Если непрерывная случайная величина Х имеет плотность распределения вероятностей , то

.

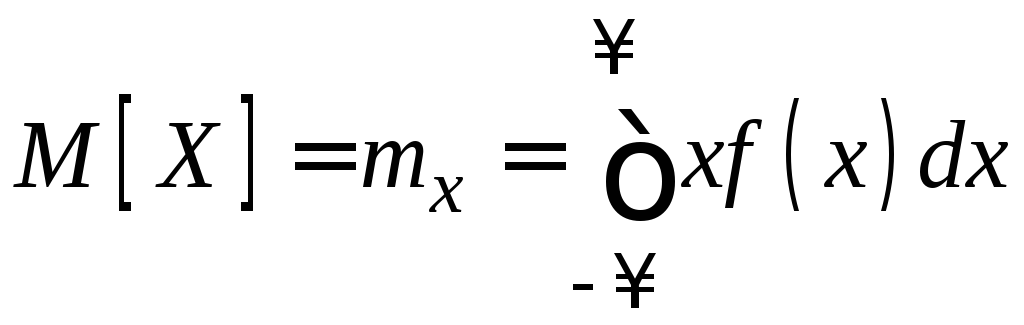Свойства математического ожидания

1. ,

2. ,

3. ,

4. , если случайные величиныX и Y независимы.

Дисперсией или рассеянием случайной величиныХ называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания

.

Величина называетсясредним квадратическим отклонением случайной величины Х.

Для непрерывных случайных величин

.

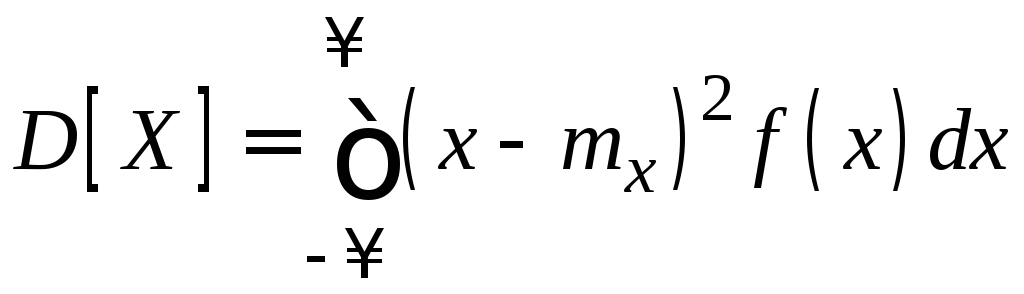Основные свойства дисперсии

1. ,

2. ,

3. ,

4. .

Пример 1. Из партии, содержащей 100 изделий, среди которых имеется 10 дефектных, выбраны случайным образом 5 изделий для проверки их качеств. Построить ряд распределения случайного числа Х – дефектных изделий содержащихся в выборке. Найти математическое ожидание и дисперсию.

Решение. Значения случайной величины принимают значения Вероятностьвычислим по формуле

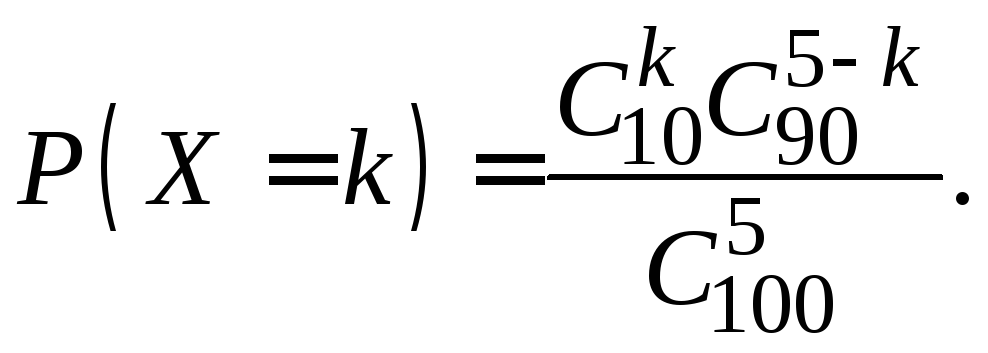
В результате получим

	0	1	2	3	4	5
	0,583	0,340	0,070	0,007	0	0

.

.

Пример 2. Производятся последовательные независимые испытания пяти приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Построить ряд распределения случайного числа испытанных приборов, если вероятность выдержать испытания для каждого из них равна 0,9. Найти математическое ожидание и дисперсию.

Решение. Значения случайной величины есть А их вероятности будут иметь значения

и ряд имеет вид

	1	2	3	4	5
	0,1	0,09	0,081	0,0729	0,6561

,

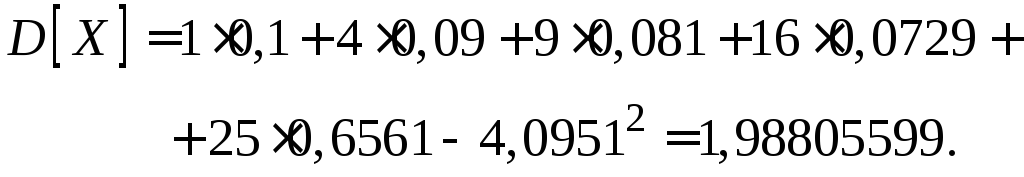
Пример 3. Непрерывная случайная величина Х задана функцией распределения . Найти: а) плотность распределения; б) математическое ожидание, дисперсию; в) вероятность.

.

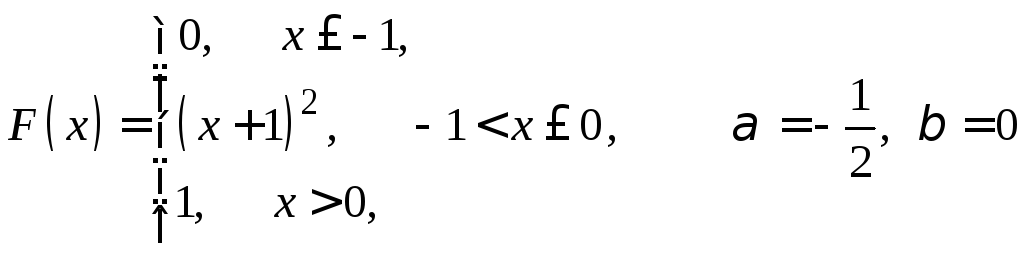Решение. а) Плотность вероятности

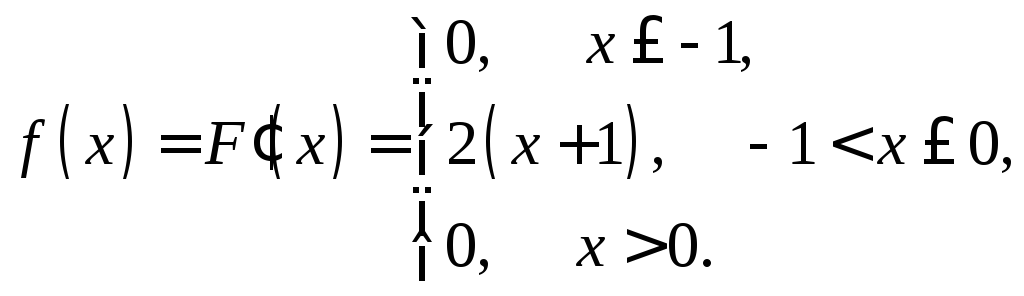
б) Математическое ожидание и дисперсию непрерывной случайной величины найдем по формулам

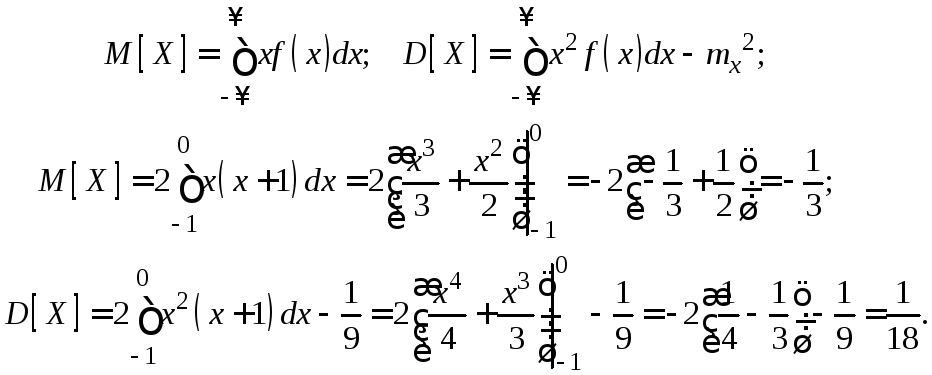
в) Вероятность попадания случайной величины Х на промежуток вычислим по одной из формул