4.2. Построение интерполяционных многочленов

Пусть на отрезке в некоторой последовательностиузловзадана функциясвоими значениями, где. Задача алгебраического интерполирования состоит в построении многочленастепени, удовлетворяющего условию интерполирования:.

Известно, что существует единственный полином степени не выше , принимающий в исходных точках заданные значения. Коэффициентыполиномаможно определить из системы уравнений:

Определитель этой системы есть определитель Вандермонда, и, следовательно, система имеет единственное решение.

Пример. Построить интерполяционный многочлен , совпадающий с функциейв точках.

Решение. Пусть , поэтому имеем

.

Отсюда .

Поэтому при.

Многочлен Лагранжа

Будем искать многочлен в виде линейной комбинации множеств степени :.

При этом потребуем, чтобы каждый многочлен во всех узлах интерполяции, за исключением одного, где он равен 1. Легко проверить, что этим условиям отвечает многочлен вида

.

Действительно, . Причислитель выражения равен 0. По аналогии получим:

,

.

Подставив эти формулы в исходный многочлен, получим:

.

Эта формула называется интерполяционным многочленом Лагранжа.

Пример. Построить интерполяционный многочлен Лагранжа , совпадающий с функциейв точках

.

Решение. Составим таблицу

х	-2	-4/3	0	4/3	2
у	0	1	2	1	0

Подставляя эти значения в формулу Лагранжа, получим:

Если функция непрерывно дифференцируема до-го порядка включительно, то остаточный член интерполяционного многочлена в форме Лагранжа имеет вид

,

где – внутренняя точка минимального отрезка, содержащего узлы интерполированияи точку.

Многочлен Ньютона с конечными разностями

Рассмотрим случай равноотстоящих узлов интерполяции, т. е. – называется шагом.

Введем понятие конечных разностей. Пусть известны значения функции в узлах . Составим разности значений функции:

Эти разности называются разностями первого порядка.

Можно составить разности второго порядка:

.

Аналогично составляются разности k-го порядка:

.

Выразим конечные разности непосредственно через значение функции:

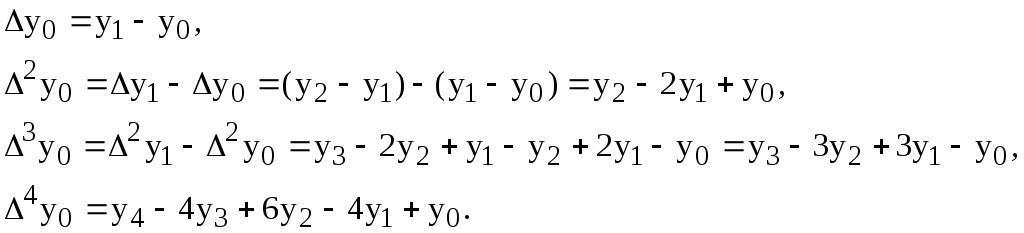
Таким образом, для любого k можно записать:

Запишем эту формулу для значений разности в узле :

.

Используя конечные разности, можно определить

.

Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в виде

.

График многочлена должен проходить через заданные узлы, то есть . Используем эти условия для нахождения коэффициентов многочлена:

Найдем отсюда коэффициенты :

Таким образом, для любого -го коэффициента формула примет вид

.

Подставляя эти формулы в выражение многочлена Ньютона, получим его следующий вид:

Полученную формулу можно записать в другом виде. Для этого введем переменную .

В этом случае

С учетом этих соотношений формулу многочлена Ньютона можно записать в виде

.

Полученное выражение может аппроксимировать данную функцию на всем отрезке изменения аргумента. Однако более целесообразно (с точки зрения повышения точности расчетов и уменьшения числа слагаемых в полученой формуле) ограничиться случаем, то есть использовать эту формулу для всех. Для других случаев вместопринять, еслипри. В этом случае интерполяционный многочлен можно записать в виде

Полученная формула называется первым интерполяционным многочленом Ньютона для интерполяции вперед. Эту интерполяционную формулу обычно используют для вычисления значений функции в точках левой половины рассматриваемого отрезка. Это объясняется следующим: разности вычисляются через значения функции, причем. Из-за этого при больших значенияхмы не можем вычислить высших порядков.

Для правой половины рассматриваемого отрезка разности лучше вычислять справа налево. В этом случае , то есть, и интерполяционный многочлен Ньютона можно получить в виде:

.

Полученная формула называется вторым интерполяционным многочленом назад.

Пример. Используя интерполяционный полином Ньютона, вычислить , где функциязадана таблицей

х	0	0,1	0,2	0,3	0,4	0,5
у	0	0,1002	0,2013	0,8045	0,4108	0,5211

Решение. Составляем таблицу конечных разностей.

х	у
0	0
		0,1002
0,1	0,1002		0,0009
		0,1011		0,0012
0,2	0,2013		0,0021		-0,0002
		0,1032		0,0010		0,0001
0,3	0,3045		0,0031		-0,0001
		0,1063		0,0009
0,4	0,4108		0,0040
		0,1103
0,5	0,5211

Для вычисления положим в интерполяционном многочлене Ньютона впередтогдаи

Пример. Задана таблица. Найти .

х
	0,2588
		0,0832
	0,3420		-0,026
		0,0806		0,0006
	0,4226		-0,032
		0,0774		0,0006
	0,5		0,038
		0,0736
	0,5736

При вычислении положим

.

При вычислении положим

.

Оценим погрешности формул Ньютона вперед и назад:

где и

где .

Формулы приближенного дифференцирования основаны на первой интерполяционной формуле Ньютона. Интерполяционный многочлен Ньютона имеет вид

,

где

Производя перемножение биномов, получим

так как , то

.

Аналогично можно вычислять производные функции любого порядка.

В некоторых случаях требуется находить производные функций в основных табличных точках. Так как табличное значение можно считать за начальное, то положив, имеем

,

Для производной многочлена Ньютона первого порядка погрешность может быть вычислена по формуле ,

где – число конечных разностей в многочлене Ньютона.

Пример. Найти функции, заданной таблично.

Решение.

х	у
50	1,6990
		0,0414
55	1,7404		-0,0036
		0,0378		0,0005
60	1,7782		-0,0031
		0,0347
65	1,8129

Здесь ;.

Вычисляя погрешность, получим:

.

Действительно, .

Таким образом, результаты совпадают до четвертого знака.