
- •«Омский государственный технический университет»
- •2. Основные этапы отыскания решения
- •Метод половинного деления
- •Метод простой итерации
- •Приведение уравнения к видудля обеспечения выполнения неравенства
- •Метод Ньютона (метод касательных)
- •6. Видоизменённый метод Ньютона
- •7. Метод хорд
- •8. Комбинированный метод
- •Решение систем линейных алгебраических уравнений
- •1. Постановка задачи
- •2. Метод простой итерации
- •3. Метод Зейделя
- •Решение систем нелинейных уравнений
- •1. Постановка задачи
- •2. Метод Ньютона для системы нелинейных уравнений
- •3. Метод итерации для нелинейной системы уравнений
- •4. Метод скорейшего спуска решения нелинейных систем
- •5. Метод скорейшего спуска для случая линейной системы
- •Приближение функций
- •1. Метод наименьших квадратов
- •2. Построение интерполяционных многочленов
- •Многочлен Лагранжа
- •Многочлен Ньютона с конечными разностями
- •Вычисление собственных значений матрицы методом Данилевского
- •Вычисление определённых интегралов
- •1. Метод Симпсона (метод парабол)
- •Численное решение дифференциальных уравнений
- •1. Постановка задачи Коши
- •2. Метод Эйлера
- •3. Модифицированные методы Эйлера
- •4. Метод Рунге – Кутта
- •Решение краевой задачи для линейного
- •Приложение
- •Библиографический список
3. Метод Зейделя
Модификацией метода простой итерации можно считать метод Зейделя.
В методе простой
итерации на
![]() -ой
итерации значения
-ой
итерации значения![]() ,
,![]() вычисляются подстановкой в правую часть
(6) вычисленных на предыдущей итерации
значений. В
методе Зейделя при вычислении
вычисляются подстановкой в правую часть
(6) вычисленных на предыдущей итерации
значений. В
методе Зейделя при вычислении
![]() используются значения
используются значения![]() ,
,
![]() ,
,
![]() ,
уже найденные на
,
уже найденные на
![]() -ой
итерации, а не
-ой
итерации, а не
![]() ,
,
![]() ,
…,
,
…,
![]() ,
как в методе простой итерации, т.е.
,
как в методе простой итерации, т.е.
![]() -е
приближение строится следующим образом:
-е
приближение строится следующим образом:
 (9)
(9)
Эти формулы являются расчетными формулами метода Зейделя.
Введем нижнюю и верхнюю треугольные матрицы:
 и
и

Матричная запись
расчетных формул (9) имеет вид:
![]() .
Так как
.
Так как![]() ,
точное решение
,
точное решение![]() исходной системы удовлетворяет равенству:
исходной системы удовлетворяет равенству:![]() .
.
Сходимость метода Зейделя. Достаточным условием сходимости метода Зейделя является выполнение неравенства:
![]() .
(10)
.
(10)
Неравенство (10)
означает, что для сходимости метода
Зейделя достаточно, чтобы любая норма
матрицы
![]() был меньше единицы.
был меньше единицы.
Если выполнено условие (10), то справедлива следующая оценка погрешности:
 ,
(11)
,
(11)
где
![]() – норма
матрицы
– норма
матрицы![]() .
.
Критерий окончания.
Если требуется найти решение с точностью
![]() ,
итерационный процесс следует закончить,
как только на
,
итерационный процесс следует закончить,
как только на![]() -ом
шаге выполнится неравенство:
-ом
шаге выполнится неравенство: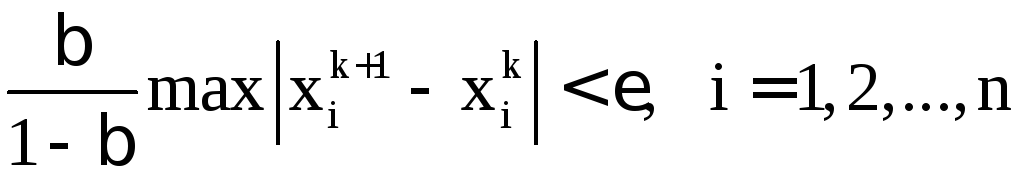 .
Поэтому в качестве критерия окончания
итерационного процесса можно использовать
неравенство
.
Поэтому в качестве критерия окончания
итерационного процесса можно использовать
неравенство![]() ,
где
,
где
 .
Если выполняется условие
.
Если выполняется условие
![]() ,
то можно пользоваться более простым
критерием окончания:
,
то можно пользоваться более простым
критерием окончания:
![]() .
.
Метод Зейделя, как правило, сходится быстрее, чем метод простой итерации. Однако, возможны ситуации, когда метод простой итерации сходится, а
метод Зейделя сходится медленнее или вообще расходится.
Пример. Применим метод Зейделя для решения системы уравнений из предыдущего примера. Первые шаги полностью совпадают с процедурой решения по методу простых итераций. Проведем теперь итерации методом Зейделя.
При
![]()
![]() .
.
При вычислении
![]() используем уже полученное значение
используем уже полученное значение![]() :
:
![]() .
.
При вычислении
![]() используем уже полученные значения и
используем уже полученные значения и![]() :
:
![]() .
.
При вычислении
![]() используем уже полученные значения
используем уже полученные значения![]() ,
,![]() ,
,![]() :
:
![]() .
.
Аналогичным образом
проведем вычисления при
![]() и
и![]() .
.
Получим:
при
![]()
![]() .
.
при
![]()
![]() .
.
Известны точные значения переменных:
![]() .
.
Сравнение с предыдущим примером показывает, что метод Зейделя сходится быстрее и дает более точный результат.
Решение систем нелинейных уравнений
1. Постановка задачи
Многие практические
задачи сводятся к решению системы
нелинейных уравнений. Пусть для вычисления
неизвестных
![]() требуется решить систему
требуется решить систему![]() нелинейных уравнений:
нелинейных уравнений:
 ,
иначе
,
иначе
![]() .
.
В отличие от решения СЛАУ не существует прямых методов решения систем нелинейных уравнений. Лишь в отдельных случаях эту систему можно решить непосредственно. Например, для случая двух неизвестных иногда удается выразить одно неизвестное через другое и таким образом свести задачу к решению одного нелинейного уравнения относительно другого.
В общем случае для решения систем нелинейных уравнений обычно используются итерационные методы.
