7. Метод хорд

Рассмотрим еще одну модификацию метода Ньютона. Пусть известно, что простой корень уравнениянаходится на отрезке, то есть. И предположим, чтопри(если это не так, то будем рассматривать уравнение). Заменим кривуюхордой.

у

А

х₂ х₁ b=x₀

а х^* x

В

Рис. 9

y

B

а=х₀ х₁ х₂ b

х^* x

А

Рис. 10

Возможны два случая: 1) (рис. 9); 2)(рис. 10 ). В первом случае конец неподвижен и последовательные приближения:

(9)

образуют ограниченную монотонно убывающую последовательность, причем .

Во втором случае неподвижен конец , а последовательные приближения:

(10)

образуют ограниченную монотонно убывающую последовательность, причем Итак, в результате получаем.

Выбор начального условия:

1. Рассматриваем только случай (иначе).

2. Начальное приближение x₀ выбираем из условия

Неподвижен тот конец, для которого знак функции совпадает со знаком ее второй производной.

Критерий окончания. Критерий окончания итераций метода хорд такой же, как и для метода Ньютона. При заданной точности вычисления нужно вести до тех пор, пока не будет выполнено неравенство.

Пример. Найти положительный корень уравнения с точностью . Отделим корень. Так как,, то. Разделим интервал пополам:, тогда.

Найдём производные: ,. Исходя из того, что, тои пользуемся формулой (10):,.

, ,.

Так как , то.

8. Комбинированный метод

Пусть , аисохраняют постоянные знаки на отрезке. Соединяя методы хорд и касательных, получаем метод на каждом этапе, которого находим значения по недостатку и значения по избытку точного корняуравнения. Пусть- последовательные приближения метода хорд,- последовательные приближения метода касательных. Пошаговая иллюстрация представлена на рис.11.

Возможны 4 случая: 1) , 2) ,

3) , 4),

которые можно свести к первому случаю.

y

x₀=а х₁ х₂

x^* х

Рис. 11

.

. .

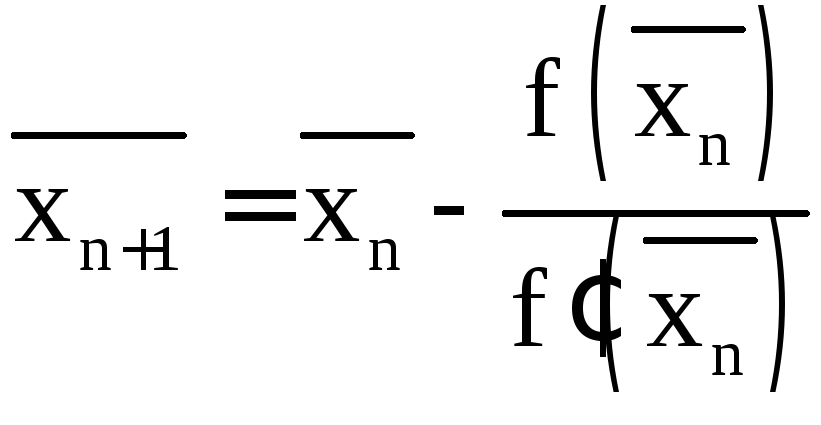Очевидно, что и.

По окончании процесса за значение корня лучше всего взять среднее арифметическое полученных значений:.

Пример. Вычислить положительный корень уравнения . Так как, то.

, на, поэтому.

.

.

; .

Так как , то

; .

Так как , то.

Решение систем линейных алгебраических уравнений

1. Постановка задачи

Требуется найти решение системы линейных уравнений:

или в матричной форме: , где

По правилу Крамера система линейных уравнений имеет единственное решение, если определитель системы отличен от нуляи значение каждого из неизвестных определяется следующим образом:, где– определитель матрицы, получаемой заме-

ной -го столбца матрицы столбцом правых частей .

Непосредственный расчет определителей для больших является очень трудоемким.

Известные в настоящее время многочисленные приближенные методы решения систем линейных алгебраических уравнений распадаются на две большие группы: прямые методы и методы итераций.

Прямые методы всегда гарантируют получение решения, если оно существуют, однако, для больших требуется большое количество операций, и возникает опасность накопления погрешностей.

Этого недостатка лишены итерационные методы, но зато они не всегда сходятся и могут применяться лишь для систем определенных классов.

Норма матрицы является некоторой обобщенной оценкой значений элементов матрицы. Для её вычисления можно использовать следующие выражения:

,

, .