Вычисление определённых интегралов

1. Метод Симпсона (метод парабол)

Заменим график функции на отрезке,,, параболой, проведенной через точки,, где - середина отрезка . Эта парабола есть интерполяционный многочлен второй степенис узлами. Нетрудно убедиться, что уравнение этой параболы имеет вид:

,

где .

Проинтегрировав эту функцию на отрезке , получим

.

Суммируя полученные выражение по , получимквадратурную формулу Симпсона (или формулу парабол):

.

Оценка погрешности. Для оценки погрешности формулы Симпсона воспользуемся следующей теоремой.

Теорема. Пусть функция имеет на отрезкенепрерывную производную четвертого порядка . Тогда для формулы Симпсона справедлива следующая оценка погрешности: , где.

Замечание. Если число элементарных отрезков, на которые делится отрезок , четно , т.е., то параболы можно проводить через узлы с целыми индексами, и вместо элементарного отрезка длины рассматривать отрезок длины. Тогда формула Симпсона примет вид:

, а вместо последней оценки будет справедлива следующая оценка погрешности:

.

Правило Рунге практической оценки погрешности.

Оценка погрешности зависит от длины элементарного отрезка , и при достаточно маломсправедливо приближенное равенство:, гдеприближенное значение интеграла. Если уменьшить шаг в два раза, то получим: .

Вычитая одно из другого, получим: , или.

Это приближенное равенство дает оценку погрешности. Вычисление этой оценки называется правилом Рунге. Правило Рунге – это эмпирический способ оценки погрешности, основанный на сравнении результатов вычислений, проводимых с разными шагами . Для формулы Симпсона, и оценка принимает вид:. Используя правило Рунге, можно построить процедуру приближенного вычисления интеграла с заданной точностью. Нужно, начав вычисления с некоторого значения шага , последовательно уменьшать это значения в два раза, каждый раз вычисляя приближенное значение. Вычисления прекращаются тогда, когда результаты двух последующих вычислений будут различаться меньше, чем на.

Пример. Вычислить .

Решение. Возьмём , тогда.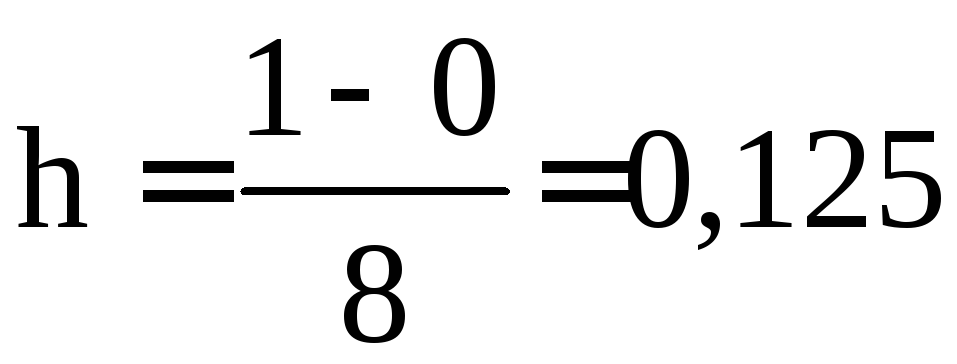

0	0			10)0,54)
1	0,125	0,984625
2	0,250		0,9411761)
3	0,375	0,876712
4	0,5		0,82)
5	0,625	0,7191
6	0,750		0,643)
7	0,875	0,566389
8	1
		3,45955	1,62818	1,5

.

.

.

Следовательно, значение интеграла можно счесть .