§ 5. Закон распределения и числовые характеристики непрерывной случайной величины

Мы знаем, что закон распределения дискретной случайной величины  задается таблицей, в которой перечислены ее возможные значения и указаны их вероятности. Для непрерывных случайных величин задание закона распределения в виде такой таблицы невозможно, так как в этом случае вероятности отдельных значений равны нулю.

Пример.

Испытание:берут наугад точку на чи­словой оси так, что значения на от­резке [0, 1] равновозможны, остальные значе­ния невозможны. Очевидно,– непре­рывная случайная величина.

Найдем

.

Закон распределения непрерывной случайной вели­чины может быть задан двумя способами:

1. с помощью функции распределения F (x);

2. с помощью плотности вероятности f (x).

Функция распределения

Пусть с испытанием связана непрерывная случайная величина .

Зафиксируем произвольное числох. В зависимости от случая возможны три исхода испытания:

 > x,=x,<x.

Каждое из этих трех событий случайно, поэтому имеет смысл говорить об их вероятности. Обозначим

F(x) =p (<x).

Функция F(x) называетсяфункцией распределения случайной величины .

Рис. 11

свойства функции распределения

1⁰. 0 ≤F(x) ≤ 1;

2⁰.F(x) монотонно не убывает (рис. 11);

3⁰.F (–) = 0,F (+) = 1;

4⁰.P(<<) =F() –F().

доказательство.

1. Это свойство вытекает из того, что вероятность любого события есть число, принадлежащее [0, 1].

2. Это свойство вытекает из того, что при увеличении хинтервал (–,х) расширяется, поэтому вероятность попадания в этот интервал не уменьшается.

3.F (–) ,

F (+) .

4. Имеем:

F() =P (<) = =

= P ( < ) + P ( = ) + P (  (, )) = F () + 0 + P (<<).

Отсюда вытекает требуемое равенство 4⁰.

Замечание.Функция распределенияF(x) имеет смысл и для дискретных случайных величин. Например, функция распределения случайной величины

 :

представляет собой кусочно-постоянную функцию, график которой изображен на рис. 12 (кружок означает, что в этом месте отсутствует точка на графике).

Рис. 12

Проверим это для случаев х>3, 2≤х< 3. В первом случае имеем

F(x) =P(<x) =P (= 1 или= 2 или= 3) =

= P(= 1) +P(= 2) +P(= 3) = 0,25 + 0,25 + 0,5 = 1.

Во втором случае

F(x) =P(= 1 или= 2) =Р(= 1) +Р(= 2) =

= 0,25 + 0,25 = 0,5.

Оставшиеся случаи 1≤ х< 2,x<1 предлагаем рассмотреть са­мостоятельно.

Плотность вероятности

[ ] Пусть с испытанием связана непрерыв­ная случайная величина.

Плотностью вероятностислучайной величины в точкехназывается предел отношения вероятности попадания в отрезок [x,x+x] к длине отрезкаxпри условии, что отрезок стягивается к точкех:

.

Нестрого говоря, плотность вероятности – это вероятность попадания в отрезок длины 1.

Свойства плотности вероятности:

1⁰.f(x) ≥ 0 при всехх.

2⁰.P((,)) =

вероятность попадания в интервал равна заштрихованной площади (рис. 13).

Рис. 13

3⁰. ПлощадьSбесконечной фигуры, ограниченной графи­ком плотностиf(x) и осью абсцисс, равна 1 (рис. 13):S= 1.

Доказательство.

1. Это свойство вытекает из того, что предел неотрица­тельной функции неотрицателен.

2. Имеем

.

Отсюда получаем

;

учтено свойство 4⁰функции распределения.

3. .

Помнить: кривая плотности вероятности показывает, как суммарная вероятность 100% распределяется по интервалам.

Замечание.Рассмотрим два крайних случая (рис.14, 15). В первом случае с вероятностью, близкой к единице, случайная величинапринимает значения, близкие кх₀, в этом случае можно без большой погрешности считать, что- неслучайная величина:х₀. Во втором случае суммарная вероятность 100% приблизительно равномерно распреде-лена по широкому спектру возможных значений, то есть в этом случаесильно случайная величина.

Рис. 14 Рис. 15

Связь между f(x) иF(x)

Пусть с испытанием связана непрерывная случайная величина с плотностью вероятностиf (x) и функцией распределенияF(x). Справедливы равенства

1⁰.;

2⁰..

доказательство.

1. по свойству плотно­сти вероятности.

2. Это свойство было доказано выше (см. доказатель­ство свойства 2⁰плотности).

Пример.Берут наугад точкуна оси так, что значения на [0, 1] равновозможны, а остальные невозможны. Найти: а) функцию распределенияF(x); б) плотность вероятностиf(x).

Решение.а)F(x) – ? [ ]

Пусть

1. х≤ 0:F(x) =P(<x) = 0.

2. 0 < x≤1:F(x) =P(<x) =P( –<≤ 0 или 0 <<x) =

= P( –<≤ 0) +P (0 <<x) = 0 + =x.

3. x > 1: F (x) = P ( < x) = P (≤ 0 или 0 <  ≤ 1 или 1 < < x) =

=

45 46

P(≤ 0) +P(0 <≤ 1) +P( 1 <<x) = 0 + 1 + 0 = 1.

Окончательно имеем

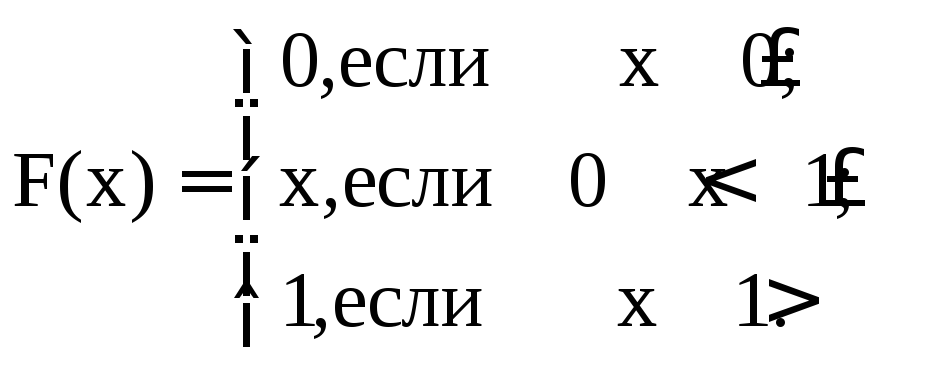
б)f (x) – ? , отсюда

Замечание.Если график плотности вероятности имеет вид, изображенный на рис. 16, то говорят, что случайная величинаравномерно распределенана [a,b].

График функции распределения для такой случайной величины имеет вид, изображенный на рис. 17.

Числовые характеристики

Напомним, что для дискретной случайной величины числовые характеристики определяются формулами:

m_ = x₁p₁ + x₂p₂ + … x_np_n = ;

D_=M[(–m_)²] = ;

.

Числовые характеристики непрерывной случайной величины определяются формулами

; ; .

Эти величины имеют такой же смысл, как в дискретном случае: математическое ожидание характеризует центральное значение случайной величины, дисперсия и СКО – разброс относительно центра. Сохраняют, как можно доказать, все свойства математического ожидания и дисперсии, доказанные в дискретном случае.

П

47 48

ример.Найти числовые характеристики для равномерно распределенной на [a,b] случайной величины.

Решение.Имеем из замечания (рис.16)

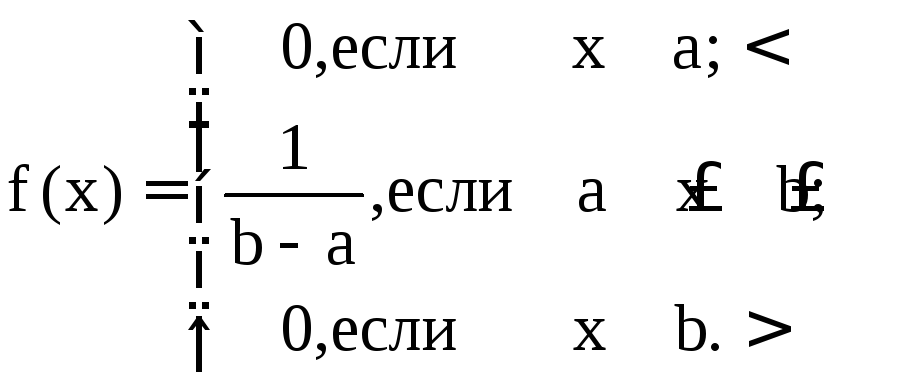
Тогда

Следовательно,

,,. (14)