§3. Математическое ожидание дискретной случайной величины

При решении инженерных задач, связанных с расчетом случая, фундаментальную роль играют так называемые числовые характеристики случайных величин: математическое ожиданиеидисперсия.математическое ожидание имеет смыслцентральногозначения случайной величины. дисперсия характеризует разброс значений случайной величины относительно центра. В этом и следующем параграфах мы изучим эти понятия для дискретной случайной величины.

Пусть - дискретная случайная величина с законом распределения

.

Математическим ожиданиемслучайной величиныназывается число:

М[] =m_=x₁·p₁+x₂·p₂+ … +x_n·p_n

(сумма произведений возможных значений на их вероятно­сти).

Пример 1.

.

мы видим: если значенияравновозможны, то математическое ожидание совпадает со средним арифметическим возможных значений.

Пример 2.

.

Помнить: математическое ожидание характеризует центральное значение случайной величины с учетом возможных значений и их вероятностей: маловероятные значения вносят малый вклад в формирование математического ожидания, наиболее вероятные значения вносят основной вклад.

Свойства математического ожидания.

1⁰.М [a ] =а.

Математическое ожидание неслучайной величины равно самой величине.

2⁰.М[а] =a M[].

Неслучайный множитель выносится за знак математиче­ского ожидания.

3⁰.M[+] =M[] +M[].

Математическое ожидание суммы случайных величин равно сумме математических ожиданий.

4⁰. Если,статистически независимы, то

M

[·] =M[] ·M[].

Доказательство.

1. Имеем: , откуда получаемm_a= 1·a=a.

2. Пусть

, тогда,

откуда М[а] =ax₁·p₁+ax₂·p₂+…+ax_n·p_n=a M[].

Для наглядности далее будем предполагать, что ,при­ни­мают два возможных значения:

;  .

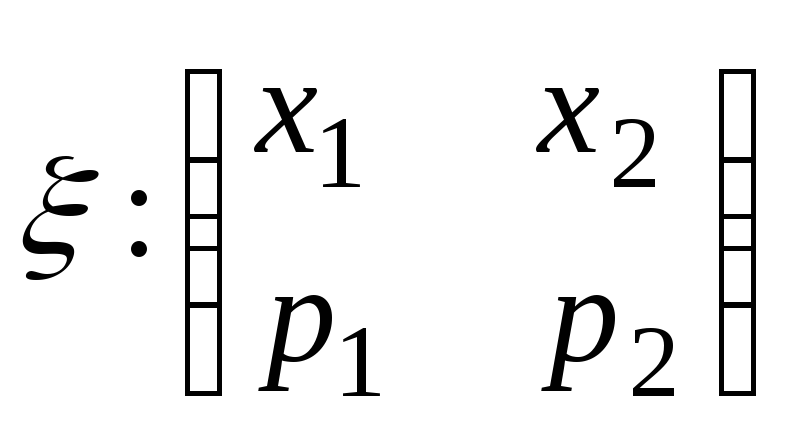3.  +  : ;

M [  +  ] ;

I₁ = p₁₁ x₁ + p₁₂ x₁ + p₂₁ x₂ + p₂₂ x₂ = (p₁₁ + p₁₂)x₁ + (p₂₁ + p₂₂)x₂.

;

доказано: р₁₁+р₁₂=р₁­, аналогично получим:р₂₁+р₂₂=р₂,

тем самым I₁=p₁x₁+p₂x₂=M[].

Также доказывается, что I₂=M[].

4. В силу теоремы умножения для независимых событий имеем: ·: .

Тогда

M[·] =p₁q₁x_1­y₁+p₁q₂x_1­y₂+p₂q₁x_2­y₁+p₂q₂x_2­y₂=

= (p₁x₁ + p₂x₂) · (q₁y₁ + q₂y₂) = M [  ] · M [  ].

§4. Дисперсия дискретной случайной величины

Пусть

;

m_=x₁·p₁+x₂·p₂+ … +x_n·p_n– математическое ожидание(центр);

 – m_– отклонениеот центра;

(–m_)²– квадрат отклоненияот центра.

Очевидно,

(–m_)² :.

Дисперсиейдискретной случайной величиныназывается матема­тическое ожидание квадрата отклонений от центра:

D[  ] = D_ = M[( – m_)²] = p₁ (x₁– m_)² + p₂ (x₂– m_)² +…+ +p_n(x_n–m_)².

пример 1.,m_= 3,

Пример 2.

,m_= 3,D_= 1.

Помнить: дисперсия характеризует разброс случайной величины относительно центра с учетом возможных значений и их вероятностей.

Свойства дисперсии:

1⁰.D[a] = 0;

2⁰.D[a] =a²D_;

3⁰. если,статистически независимы, то

D[+] =D[] +D[].

4⁰.D_=M[²] – .

доказательство.

Первое и второе свойства непосредственно вытекают из определения и соответствующего свойства математического ожидания (доказать самостоятельно).

3⁰.D[+] =M[(+–m_{ + })²] =m [(+–m_– –m_)²] =M[(–m_+–m_)²] =M[(–m_)² + (–m_)²+ + 2(–m_)(–m_)] =M[(–m_)² ] +M [(–m_)²] + 2M[– –m_ ]·M[–m_] =D_+d_+2(m_–m_)(m_–m_) =D_+d_,что и требовалось.

Здесь существенно использовалась статистическая независимость случайных величин –m_,–m_.

4⁰.D_=M [(– m_)² ] = M [ ² – 2 m_ +] = M [ ²] –

– 2 M [ ]· m_ + = M [ ²] – .

Величина

называется среднеквадратическим отклонением(СКО) случайной величины .Очевидно,_имеет тот же смысл, что иD_– характеризует разброс случайной величины относительно центра с учетом возможных значений и их вероятностей. СКО имеет ту же физическую размерность, что и случайная величина.