§3. Ковариация двух случайных величин. Коэффициент корреляции
1. Пусть с испытанием связаны случайные величины 1,2с числовыми характеристиками (а1,1), (а2,2).Ковариацией случайных величин 1,2 называется число
cov(1,2) =M[(1–a1) (2–a2)].
Из определения следует: в дискретном случае
(22)
в непрерывном случае
cov(1,2) =
.
(23)
Укажем основные свойства ковариации.
10.cov(, ) = d.
20.cov(1, 2) =M[1, 2]-а1а2.
30. Если1, 2независимы, тоcov(1, 2)=0.
40. |cov(1,2) | ≤1·2.
50. Если в 40 имеет место равенство: |cov(1,2)| =1·2, то между1,2имеется линейная функциональная связь:
А1+В2+С= 0 при некоторых А,В,С.
Геометрически это означает, что реализации случайной точки (1,2) с достоверностью ложатся на прямуюАх+By+С= 0.
Докажем свойства 10– 40.
1. cov (, )= M [( – a) ( – a)]= d.
2. cov (1, 2) = M [(12– a12 – a21 + a1a2] =M [1·2] – a1M [2] – a2M [1] + a1 · a2 = M [1 · 2] – a1 · a2 – a2· a1 + a1 · a2 = M [1 · 2] – a1 · a2.
3. Из независимости 1,2следует независимость случайных величин1–a1, 2–a2. Так как математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий, то имеем
cov (1, 2) = M (1 – a1) M (2 – a2)=(M[1]– a1) (M[2]– a2)= =(a1 – a1)( a2 – a2)=0.
4. Доказательство этого свойства проведем для непрерывного случая. Представим указанную в начале параграфа интегральную формулу для ковариации в виде
где обозначено
(для удобства записи пределы интегрирования опущены). Воспользуемся известным фактом математического анализа-неравенством Буняковского: для любых непрерывных φ1, φ2 и любой областиD
Отсюда следует:
Имеем:
В этом вычислении учтено свойство 50 плотности вероятностиf(х,у)и определение дисперсии непрерывной случайной величины. Аналогично найдем
Таким образом
что и требовалось.
2. На практике при изучении совместных свойств случайных величин, как правило, пользуются нормированной ковариациейиликоэффициентом корреляции:
(24)
Из свойств ковариации вытекают следующие свойства коэффициента корреляции.
10. -1 ≤r ≤ 1.
20. Еслиr =1, то между1,2имеется линейная функциональная связь (рис.26). Уравнение прямой вычисляется по параметрам (а1, а2, σ1, σ2,r).
30. Если1,2независимы, тоr= 0.
Замечание 1.Из 10-30 следует, что коэффициент корреляции (и, соответственно, ковариации) является некой мерой связи между1,2. Более подробные рассмотрения показывают следующее. Если׀ r׀ 1, то связь между1,2близка к линейной функциональной: реализации случайной точки (1,2) с практической достоверностью ложатся вблизи заранее прогнозируемой прямойАх+By+С= 0. Еслиr0, то либо1,2независимы, либо связь между ними имеется, но далека от линейной связи.
Помнить: коэффициент корреляции является мерой линейной связимежду случайными величинами.
Замечание 2. В силу свойства 30 из независимости случайных величин1,2 следуетr=0. Обратное утверждение неверно: имеются примеры, когдаr=0 и при этом1,2 зависимы. Укажем важный частный случай, когда изr= 0 следует независимость1,2. Будем говорить, что случайные величины1,2 имеютсовместное нормальное распределениес параметрами (а1, σ1,а2, σ2,r), если плотность вероятности случайной точки (1,2) дается формулой
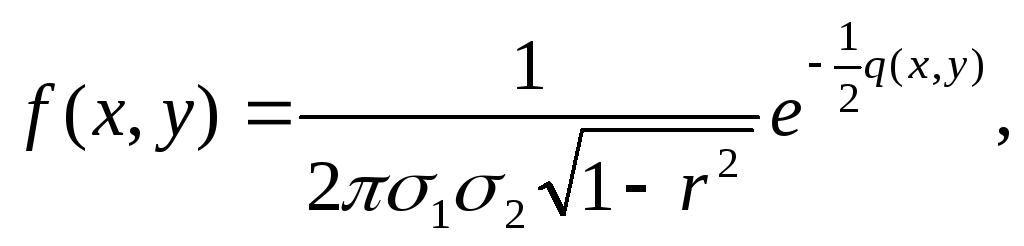(25)
где
Можно
показать, чтоа1, а2– математические ожидания, σ1, σ2– СКО случайных величин1,2,r-
коэффициент корреляции.
(26)
где
,
Нетрудно показать, используя свойство 50 плотности вероятностиf(x,y),чтоf1(x), f2(y)– плотности вероятности случайных величин1,2; поэтому в силу свойства 60 f(x,y) 1,2 независимы.
Помнить: в нормальном случае коэффициент корреляции является точной мерой связи между1,2.
Замечание 3. Числа (а1, σ1,а2, σ2,r) называются числовыми характеристиками случайной точки (1,2). Пары (а1, σ1), (а2, σ2) характеризуют отдельно1,2;rявляется мерой связи между1,2. В непрерывном случае параметрrвычисляется по формулам (23), (24), остальные параметры – по формулам
(27)
Пример 1.Найти числовые характеристики случайной точки (1,2) в ситуации примера на стр.57.
Решение.Имеем
1=2 =
.
Коэффициент корреляции найдем по формулам (22), (24) с учетом свойства 20для ковариации. Имеем
M[1·2]
=
=
откуда
.
Пример 2.Найти числовые характеристики случайной точки (1,2) в ситуации примера на стр. 60.
Решение.Имеем
а1=а2= 1,D1=D2=
,1=2
=
.
Коэффициент корреляции найдем по формулам (23), (24)
cov(1,2)
=
откуда
.