Глава 12. Устойчивость решений систем дифференциальных уравнений

12.1. Понятие устойчивости по Ляпунову

Рассмотрим нормальную систему дифференциальных уравнений:

. (12.1)

Пусть – решение системы (12.1), соответствующее начальным условиям, или.

Кроме того, – решение системы (12.1), соответствующее измененным начальным условиям, или.

ОПРЕДЕЛЕНИЕ. Решение системы (12.1) называетсяустойчивым по Ляпунову, если для любого существуеттакое, что из совокупности неравенствследуют неравенства.

Из определения следует, что если – устойчивое решение, товсякое решение, достаточно близкое к нему в начальный момент , остается близким к нему с ростом.

ОПРЕДЕЛЕНИЕ. Решение системы (12.1) называетсяасимптотически устойчивым по Ляпунову, если существует такое, что из совокупности неравенствследует, что

.

Из определения следует, что всякое решение, достаточно близкое к в начальный момент, неограниченно сближается с ним с ростом.

ПРИМЕР. Рассмотрим дифференциальное уравнение первого порядка , где– параметр. Очевидно, что это уравнение имеет тривиальное решение, удовлетворяющее при любомначальному условию

Исследуем на устойчивость это решение. Для этого зададим другое начальное условие и найдем решение, которое ему удовлетворяет.

–общее решение уравнения.

–искомое частное решение.

Отсюда .

1. Пусть , поэтому каким бы близким к нулю ни было значение,неограниченно возрастает, то есть найденное решение неограниченно удаляется от решения. А это по определению означает, что принулевое решение свойством устойчивости не обладает, или является неустойчивым (рис.5).

2. Пусть при всех, значит. Зададим. Тогда приполучим, что если, то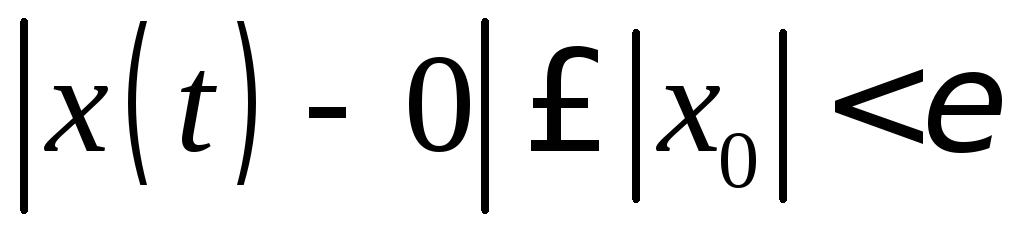. Определение устойчивости выполнено, поэтому принулевое решение устойчиво по Ляпунову (рис.6, 7).

Заметим, что если , то, то есть в этом случае нулевое решение асимптотически устойчиво (рис.7).

ОПРЕДЕЛЕНИЕ. Решение системы (12.1) называетсяасимптотически устойчивым в целом, если гдерешение, определяемоелюбыми начальными условиями, а не только значениями, близкими к начальным значениям ,.

Как было показано выше, при нулевое решение д.у.асимптотически устойчиво в целом.

Рассмотрим систему уравнений (12.1). Каждому решению (12.1) соответствует интегральная кривая , илитраектория. Если эта система имеет не зависящее от решение, то соответствующая траектория будет точкой. Она называетсяточкой покоя системы (12.1), или ее положением равновесия. В частности, тривиальное решение называется точкойпокоя этой системы, расположенной в начале координат (она существует, лишь если ).

Сформулируем определение устойчивой точки покоя, расположенной в начале координат.

ОПРЕДЕЛЕНИЕ. Тривиальное решение системы (12.1) называется устойчивым по Ляпунову, если для любого существуеттакое, что из совокупности неравенствследуют неравенства.

Такому определению можно дать другую, эквивалентную формулировку.

ОПРЕДЕЛЕНИЕ. Точка покоя, расположенная в начале координат, называется устойчивой по Ляпунову, если для любого существуеттакое, что из неравенстваследует, что

.

Геометрически это означает, что если тривиальное решение устойчиво, то всякая траектория, определяемая начальной точкой и начинающаяся внутри круга (сферы) радиуса, не покидает прикруга (сферы) радиуса(рис. 8)c центром в начале координат.

ОПРЕДЕЛЕНИЕ. Тривиальное решение системы (12.1) называется асимптотически устойчивым, если существует такое, что из совокупности неравенствследует, что, или, другими словами, если из неравенстваследует, что

.

Геометрическая иллюстрация этого определения – рис. 9: если тривиальное решение асимптотически устойчиво, то любая траектория, которая определяется начальной точкой в круге радиуса, не только не выйдет из этого круга, но и будет стремиться к его центру.

Оказывается, что исследование на устойчивость любого частного решения системы (12.1) можно заменить исследованием устойчивости тривиального решения некоторой другой системы. Покажем это.

Пусть – исследуемое решение. Введем новую переменную. Если решениеустойчиво, то любое решение, близкое к нему в начальный момент, остается близким к нему и при. Отсюда следует, что если приблизко к началу координат, тоне удаляется оти с ростом.

Выясним, какой системе уравнений удовлетворяет функция , еслиудовлетворяет (12.1):

. (12.2)

Система (12.2) имеет тривиальное решение . Если оно устойчиво, то устойчиво любое частное решение системы (12.1).

Рассмотрим линейную неоднородную систему

(12.3)

и соответствующую ей однородную систему линейных дифференциальных уравнений

. (12.4)

Исследуем на устойчивость частное решение системы (12.3) . Пусть– это отклонение точек на произвольной траекторииот соответствующих точек исследуемой траектории. Такое отклонение называетсявозмущением.

,

так как удовлетворяет (12.3).

Таким образом, если решение неоднородной системы (12.3) устойчиво, то устойчиво и тривиальное решение соответствующей однородной системы (12.4) и наоборот: из устойчивости нулевого решения однородной системы (12.4) следует устойчивость решениянеоднородной системы (12.3).

Итак, все частные решения неоднородной системы (12.3) в смысле устойчивости ведут себя так же, как тривиальное решение соответствующей однородной системы (12.4). Поэтому исследование устойчивости произвольного решения системы (12.3) можно заменить исследованием устойчивости точки покоя, расположенной в начале координат, однородной системы (12.4).

ПРИМЕР. Исследовать на устойчивость решения дифференциального уравнения .

Это линейное однородное уравнение, оно имеет тривиальное решение , которое удовлетворяет начальному условию.

Исследуем устойчивость этого решения. Изменим начальное условие: – и найдем соответствующее ему решение.

.

Так как , то тривиальное решение асимптотически устойчиво в целом, а это означает, что асимптотически устойчивы в целом и все частные решения данного дифференциального уравнения.

ПРИМЕР. Исследовать на устойчивость решения системы дифференциальных уравнений .

Сведем систему к одному дифференциальному уравнению 2-го порядка: из второго уравнения получаем

.

Тогда .

Итак, – общее решение системы.

Очевидно, что данная система имеет точку покоя, расположенную в начале координат. Такое решение удовлетворяет условию . Чтобы исследовать его устойчивость, рассмотрим произвольное решение, определяемое начальным условием. Оно имеет вид.

При достаточно малых значениях значениятакже будут достаточно малы, потому что. А это означает, что тривиальное решение и вместе с ним все частные решения данной системы устойчивы, хотя асимптотической устойчивости нет.

ПРИМЕР. Исследовать на устойчивость решения дифференциального уравнения .

Найдем общее решение: характеристическое уравнение имеет вид

.

Отсюда следует, что нулевое решение этого дифференциального уравнения асимптотически устойчиво в целом, а это значит, что асимптотически устойчивы в целом не только все частные решения данного однородного дифференциального уравнения, но и все частные решения неоднородного уравнения.

ПРИМЕР. Исследовать на устойчивость решения дифференциального уравнения .

Составим и решим характеристическое уравнение:

.

Отсюда – ф.с.р.. Зададим следующее начальное условие:– соответствующее частное решение. При достаточно малом значении, то есть траектория, начинаясь вблизи начала координат, с ростомнеограниченно от него удаляется. По определению это означает, что тривиальное решениеустойчивым не является, значит, неустойчивы и все частные решения данного дифференциального уравнения, а также неоднородного уравнения.

Из рассмотренных примеров можно заключить, что для линейных уравнений и систем дифференциальных уравнений с постоянными коэффициентами устойчивость или неустойчивость их решений зависит от вида корней соответствующих характеристических уравнений. Исследуем этот вопрос подробно.