Глава 11. Системы дифференциальных уравнений

11.1. Основные определения

Любое дифференциальное уравнение -го порядка можно свести к системе дифференциальных уравнений первого порядка, вводя новые переменные.

ПРИМЕР. Рассмотрим дифференциальное уравнение

.

Пусть ,, тогда уравнение равносильно системе трех дифференциальных уравнений первого порядка относительно неизвестных функций:

Уравнение 2-го порядка можно свести к системе двух дифференциальных уравнений первого порядка:

Рассмотрим систему дифференциальных уравнений первого порядка

(11.1)

где – вектор-столбец неизвестных,– вектор-столбец правых частей.

Система дифференциальных уравнений вида (11.1) называется нормальной: производные 1-го порядка стоят только в левых частях уравнений, правые части производных не содержат.

ОПРЕДЕЛЕНИЕ. Порядком системы дифференциальных уравнений называется сумма порядков уравнений, входящих в систему.

Система дифференциальных уравнений (11.1) – система -го порядка.

ОПРЕДЕЛЕНИЕ. Решением системы (11.1) называется совокупность функций, подстановка которых в систему обращает каждое ее уравнение в тождество.

Если полагать, что – координаты движущейся точки, то решение системы– закон ее движения, а кривая, заданная параметрически– траектория движения. Эту кривую также называют интегральной кривой системы (11.1).

Производная характеризует скорость движения. Если в системе (11.1) правая часть не зависит от, то есть, то скорость не меняется с течением времени. Такое движение называетсяустановившимся, а система – автономной или стационарной.

ТЕОРЕМА Коши. Пусть функции и их производныенепрерывны в некоторой областиизменения переменных. Тогда для любой точкисуществует, причем единственное, решение системы (11.1), удовлетворяющее начальному условию

, или

Без доказательства.

ОПРЕДЕЛЕНИЕ. Нормальная система дифференциальных уравнений называется линейной, если неизвестные функции и их производные входят в нее линейно.

Такая система имеет вид:

или в матричной форме

, (11.2)

где .

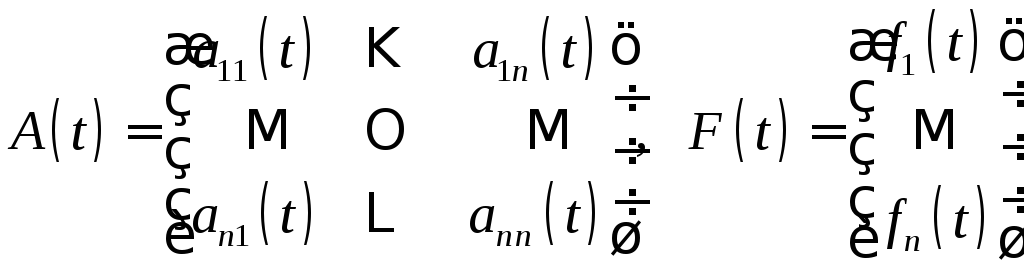Линейная система вида

(11.3)

называется однородной. Система (11.2), если ее правая часть ,неоднородная.

ТЕОРЕМА (о линейной комбинации решений линейной однородной системы).

Пусть и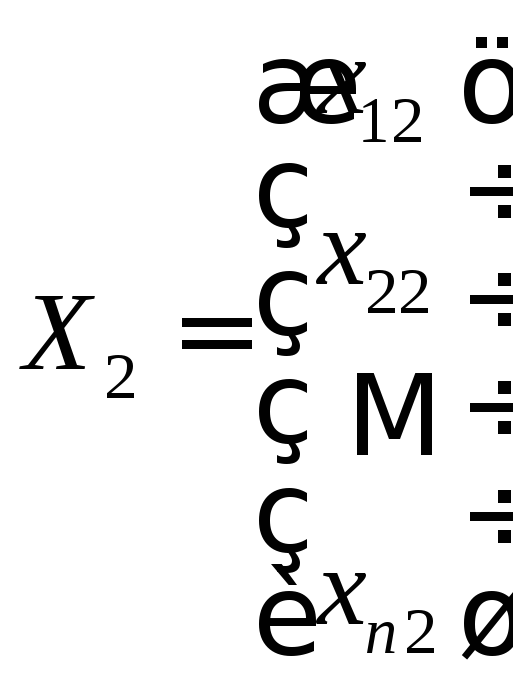– два решения линейной однородной системы (11.3). Тогда для любых постоянныхивектор-функция– также решение системы (11.3).

Доказать самостоятельно.

ЗАМЕЧАНИЕ. Если (– мнимая единица) – решение системы (11.3), тои– также решения системы (11.3).

Действительно, так как – решение системы (11.3), то

.

Отсюда по определению равенства комплексных чисел получаем: и.

ОПРЕДЕЛЕНИЕ. Решения 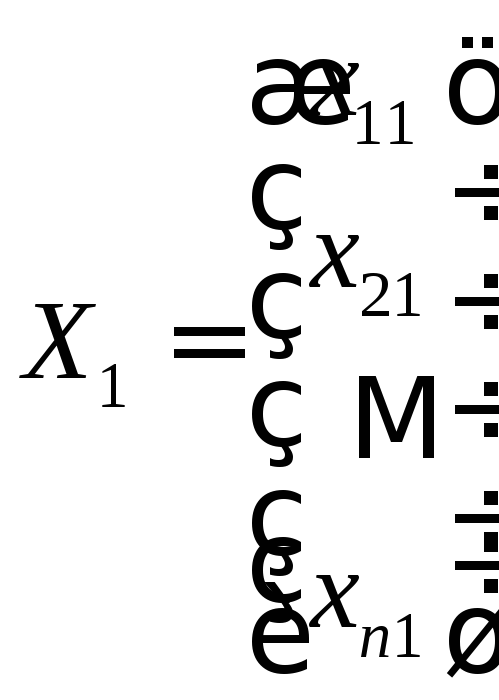, …,однородной системы (11.3) называютсялинейно независимыми, если определитель Вронского

.

ОПРЕДЕЛЕНИЕ. Вектор-функция называетсяобщим решением системы (11.1), если

1. при любых значениях постоянных функция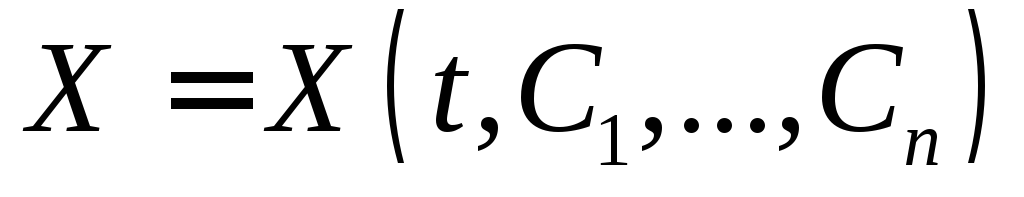– решение (11.1);

2. какое бы начальное условие , удовлетворяющее условиям теоремы Коши, ни было задано, найдется единственный набор постоянных, такой что– решение, удовлетворяющее этому начальному условию.

ТЕОРЕМА (о структуре общего решения линейной однородной системы дифференциальных уравнений). Пусть – линейно независимые решения системы (11.3) с непрерывными коэффициентамиТогда ее общее решение имеет вид:, где– произвольные постоянные.

ДОКАЗАТЕЛЬСТВО. По теореме о линейной комбинации решений вектор-функция является решением системы (11.3).

Зададим начальное условие, удовлетворяющее условиям теоремы Коши

–система линейных уравнений, основной определитель которой , так по условию решениялинейно независимы. Значит, система имеет единственное решение, а– решение (11.3), удовлетворяющее поставленному начальному условию.

Что и требовалось доказать.

ТЕОРЕМА (о структуре общего решения линейной неоднородной системы дифференциальных уравнений). Пусть – некоторое частное решение линейной неоднородной системы дифференциальных уравнений (11.2), а – общее решение соответствующей однородной системы (11.3). Тогда общее решение системы (11.2) имеет вид:.

Доказать самостоятельно.