Ранг матрицы. Элементарные преобразования

ОПРЕДЕЛЕНИЕ. Минором порядка матрицы А называется определитель-го порядка, составленный из элементов матрицы А, стоящих на пересечении произвольно выбранныхстрок истолбцов без изменения порядка их следования.

ПРИМЕР. Рассмотрим матрицу .

Миноры первого порядка – каждый элемент матрицы .

Миноры второго порядка: и так далее.

Матрица имеет всего 18 миноров второго порядка.

Миноры третьего порядка:

Миноров четвертого порядка у этой матрицы нет.

ТЕОРЕМА. Если все миноры -го порядка матрицаА равны нулю, то равны нулю и все миноры старших порядков, если они существуют.

ДОКАЗАТЕЛЬСТВО. Рассмотрим минор порядка . Это определитель-го порядка, который ( по свойству 7 ) можно разложить по элементам некоторой строки (столбца ). В разложении будут алгебраические дополнения, которые с точностью до знака совпадают с минорами- го порядка и по условию равны нулю. Поэтому равен нулю и рассматриваемый минор порядкаАналогично равны нулю и миноры старших порядков,…, если они существуют, что и требовалось доказать.

ОПРЕДЕЛЕНИЕ. Рангом матрицы А называется такое целое число , что среди ее миноров-го порядка есть хотя бы один ненулевой, а все миноры порядка () равны нулю.

Из доказанной теоремы следует, что, другими словами, ранг матрицы – это наивысший порядок отличного от нуля минора.

Будем обозначать ранг матрицы.

Ранг матрицы равен нулю тогда и только тогда, когда ее миноры равны нулю, то есть если матрица нулевая.

ПРИМЕР.

Матрица , очевидно, имеет ненулевой минор второго порядка, например,, но все ее миноры третьего порядка – их всего 16 – равны нулю, поэтомуДля того чтобы обнаружить этот факт без трудоемких вычислений, введем понятие элементарных преобразований.

ОПРЕДЕЛЕНИЕ. Элементарными преобразованиями матрицы называются следующие действия:

1) умножение любой строки на число ;

2) перемена местами двух строк;

3) прибавление ко всем элементам строки соответствующих элементов другой строки, умноженных на одно и то же число;

4) отбрасывание нулевой строки;

5) отбрасывание одной из двух пропорциональных строк;

6) те же преобразования со столбцами.

ТЕОРЕМА. Элементарные преобразования не изменяют ранга матрицы. С их помощью всякую матрицу можно привести к диагональному виду, и ее ранг равен количеству ненулевых элементов на главной диагонали (без доказательства).

Покажем теперь, что ранг матрицы F из последнего примера равен 2.

.

При переходе от кииспользовались элементарные преобразования 3), 5), 6): первую строкуприбавили ко второй и четвертой, затем отбросили две из трех пропорциональных строк; далее первый столбецприбавили ко второму и четвертому с коэффициентами 2 и (-4) соответственно и два из трех пропорциональных столбцов отбросили. По теореме.

Вычислить , очевидно, можно было, получив лишь матрицу, не выполняя дальнейших преобразований.

Исследование произвольных систем линейных уравнений

Рассмотрим систему m линейных уравнений с n неизвестными.

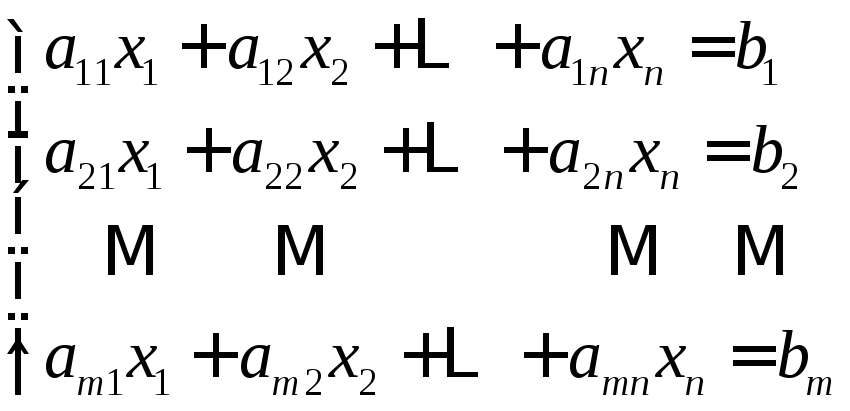(1.14)

Матрица называется основной матрицей системы (1.14), а

–расширенной матрицей системы (1.14).

ОПРЕДЕЛЕНИЕ. Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.

ОПРЕДЕЛЕНИЕ. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений у нее более одного.

ПРИМЕР.

ТЕОРЕМА. (Кронекера-Капелли, критерий совместности системы линейных уравнений) Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг ее основной матрицы был равен рангу расширенной (без доказательства).

ТЕОРЕМА (о числе решений). Пусть выполнены условия совместности системы линейных уравнений. Тогда, если , где– число неизвестных, то система имеет единственное решение. Если, то система имеет бесконечное множество решений, при этом () переменных задаются свободно, тогда оставшиесяпеременных определятся единственным образом (без доказательства).