Обратная матрица

ОПРЕДЕЛЕНИЕ. Матрица называетсяобратной для матрицы , если она вместе судовлетворяет условию:, где– единичная матрица.

Из определения следует, что и– перестановочные, значит, обратная матрица существует лишь для квадратной матрицы(прямоугольные матрицы обратных не имеют).

ОПРЕДЕЛЕНИЕ. Квадратная матрица называетсяневырожденной, если . Если, тоназываетсявырожденной.

ПРИМЕР.

по свойству 6 определителей, то есть – вырожденная.

, значит, – невырожденная.

ТЕОРЕМА. Всякая невырожденная матрица имеет обратную, причем одну.

ДОКАЗАТЕЛЬСТВО. Рассмотрим для определенности квадратную матрицу третьего порядка:

.

Покажем, что матрица вида является обратной для(– алгебраические дополнения элементовматрицы,).

По условию – невырожденная, т.е.существует. Найдем произведение, используя свойства 7,8 определителей:

Аналогично доказывается, что .

Следовательно, по определению матрица является обратной для.

Докажем единственность обратной матрицы.

Пусть невырожденная матрица имеет две обратные:и. Тогда по определению

(1.8)

(1.9)

Умножим (1.8) слева на :.

Используя свойство 2 умножения матриц и равенство (1.9), получим:

.

Таким образом, обратная матрица единственна, что и требовалось доказать.

Обратная матрица для матрицы - го порядка имеет вид:

.

ПРИМЕР. Найти матрицу, обратную для .

=3существует.

Проверка:

ПРИМЕР. Найти матрицу, обратную для

существует.

Проверка:

Аналогично проверяется, что .

Крамеровские системы уравнений

Рассмотрим систему линейных уравнений с неизвестными:

(1.10)

Матрица, составленная из коэффициентов системы (1.10)

,

называется основной матрицей системы (1.10), –основной определитель системы (1.10).

ОПРЕДЕЛЕНИЕ. Система линейных уравнений называется Крамеровской, если

1) число уравнений равно числу неизвестных;

2) основной определитель не равен нулю.

Рассмотрим матрицы 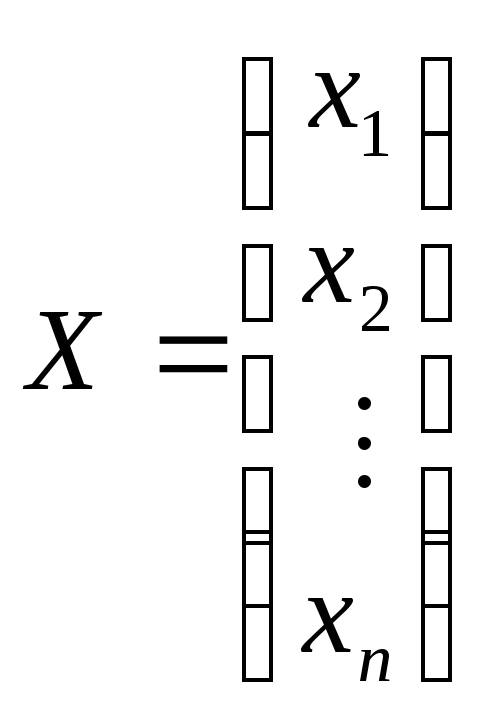и: Х – столбец неизвестных,

В – столбец правых частей. Очевидно, что система (1.10) может быть записана в виде матричного уравнения

(1.11)

ОПРЕДЕЛЕНИЕ. Совокупность чиселназываетсярешением системы (1.10), если каждое из уравнений системы обращается в верное числовое равенство при подстановке в него чисел вместо соответствующих переменных

ТЕОРЕМА. Всякая Крамеровская система имеет решение, причем одно.

ДОКАЗАТЕЛЬСТВО. По условию Значит, для основной матрицы А системы существует обратная матрица. Умножим (1.11) наслева:

(1.12)

По формуле (1.12) определяется каждое из неизвестных то есть находится решение системы (1.10), причем оно единственно, так как единственна обратная матрица

ЗАМЕЧАНИЕ. Способ решения системы (1.10) по формуле (1.12) называется матричным способом решения системы линейных уравнений.

ПРИМЕР. Решить систему уравнений матричным способом:

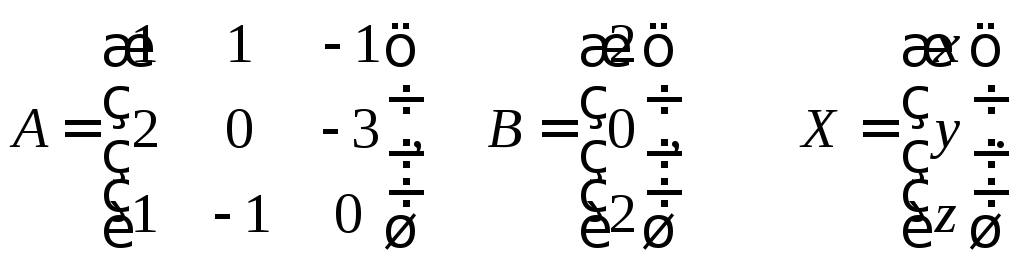
В предыдущем примере было показано, что , значит, систему матричным способом решить можно. Там же была найдена обратная матрица

Таким образом, Проверкой убеждаемся, что решение найдено верно.

ЗАМЕЧАНИЕ. Матричный способ удобен, когда надо решить несколько Крамеровских систем, которые отличаются только правыми частями.

Вернемся к равенству (1.12). Из него следует, что

,

поэтому , (1.13)

где ,– определитель матрицы, полученной из А заменой ее -го столбца на столбец правых частей системы (1.10) , = 1,2,…,. Формулы (1.13) называютсяформулами Крамера.