Приведение общих уравнений прямой в пространстве к каноническому виду

Рассмотрим прямую , заданную общими уравнениями (3.42) в пространстве:

.

Привести эти уравнения к каноническому виду можно двумя способами:

1) найти координаты какой-либо точки , лежащей на, ее направляющий вектори написать уравнения (3.45);

2) найти координаты двух точек, лежащих на , и воспользоваться уравнениями (3.46).

1 способ. Координаты точки – любое частное решение системы линейных уравнений (3.42). Эта система имеет бесконечное множество решений, так как ранги основной и расширенной матриц, а число неизвестных.

–направляющий вектор прямой , поэтому, где– нормаль плоскости, а– нормаль плоскости. Из определения векторного произведения векторов следует, что тогда. Так как– произвольный вектор, параллельный, то будем считать, что.

ПРИМЕР. Привести уравнения прямой к каноническому виду.

Найдем какое-нибудь частное решение этой системы: пусть, например, , то есть точкалежит на прямой.

.

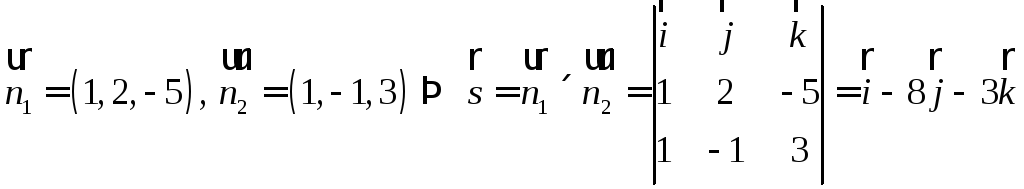Таким образом, – канонические уравнения данной прямой.

2 способ. Найдем два произвольных частных решения системы уравнений, задающей прямую.

В рассмотренном примере . Пусть теперь

,

тогда – направляющий вектор прямой, который отличается от найденного ранее только знаком. Поэтому уравнениясовпадают (с точностью до знака) с уже найденными.

Угол между прямой и плоскостью

ОПРЕДЕЛЕНИЕ. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.

Пусть в некоторой пдск заданы плоскость

и прямая

(рис. 50).

Рис. 50
Рис. 51	1) – условие перпендикулярности прямой и плоскости (рис. 51).
Рис. 52	– условие параллельности прямой и плоскости (рис. 52).

Определение общих точек прямой и плоскости

Чтобы найти общие точки прямой и плоскости, надо решить систему линейных уравнений:

.

Решение этой системы будет наименее трудоемким, если перейти к параметрическим уравнениям прямой (3.44):

(3.47)

1) Пусть . Это значит, что прямая не параллельна плоскости, а потому они имеют одну общую точку. Из (3.47) найдем

и по формулам (3.44) – их точку пересечения.

2) Пусть . Это означает, что в (3.47) решений нет: выполнено условие параллельности прямой и плоскости, при этом точка, но не лежит в плоскости, значит, прямая и плоскость общих точек не имеют.

3) Пусть . Тогда любое– решение (3.47) и система имеет бесконечно много решений: выполнено условие параллельности прямой и плоскости и точка, лежащая на прямой, лежит в плоскости. Это значит, что прямая лежит в плоскости, то есть имеет с ней бесконечное множество общих точек.

ПРИМЕР. Найти проекцию точки на плоскость(рис. 53).

Пусть прямая проходит через точкуМ перпендикулярно плоскости . Точка ее пересечения с плоскостью и будет искомой проекцией. В качестве направляющего вектораможно взять нормаль к плоскости. Напишем канонические уравнения прямой (3.45):

M P Рис. 53

. Перепишем их в параметрическом виде (3.44), чтобы найти точку Р пересечения прямой МР и плоскости .

. Подставим в уравнение плоскости:

, то есть – искомая проекция.