Произведение линейных преобразований

Рассмотрим матрицы и. Каждая из них определяет линейное преобразование плоскости. Если– некоторая точка плоскости, то под действием линейного преобразованияс матрицейона перейдет в точку:

. (3.27)

В свою очередь точка под действием линейного преобразованияс матрицейперейдет в точку:

. (3.28)

Такое последовательное выполнение линейных преобразований называется их произведением: .

Покажем, что произведение линейных преобразований также линейное преобразование, и найдем его матрицу. Подставим (3.27) в (3.28):

.

То есть

(3.29)

(3.29) – система линейных уравнений, а потому произведение линейных преобразований линейно. Матрица (3.29) имеет вид:

.

Таким образом, матрица произведения линейных преобразований равна произведению их матриц. Само же правило умножения матриц, сформулированное в гл.1, находит объяснение в этом выводе.

Приведение квадратичной формы к каноническому виду

ОПРЕДЕЛЕНИЕ. Квадратичной формой относительно двух переменных иназывается однородный многочлен второй степени:

. (3.30)

Уравнение задает на плоскости кривую второго порядка, причем, так как вместе с точкой, лежащей на этой кривой, ей принадлежит и точка, кривая симметрична относительно начала координат, то есть является центральной кривой (эллиптического или гиперболического типа).

Предположим, что уравнение задает впдск ХОУ эллипс. Если , то это уравнение не является каноническим уравнением эллипса, а потому, хотя О(0, 0) – его центр, оси симметрии не совпадают с ОХ и ОУ (рис. 43). Тем не менее, заметим, что если оси системыповернуть на

y x О Рис. 43

угол , то в системеэллипс будет задаваться каноническим уравнением: кривая симметрична относительнои. Найдем линейное преобразование, соответствующее этому повороту. Матрица называетсяматрицей квадратичной формы (3.30).

Пусть .

Вычислим

.

Таким образом, квадратичная форма может быть записана в матричном виде:

(3.31)

Пусть – координаты точек плоскости в системе, а– координаты точек плоскости в новой системе, гдекривая задается каноническим уравнением. Переход от “старых” координат к “новым” будем искать в виде

. (3.32)

(3.32) – ортогональное линейное преобразование с матрицей

; .

По определению ортогональной матрицы

(3.33)

(В результате ортогонального преобразования не происходит изменение площадей фигур, то есть фигуры не деформируются.)

Чтобы узнать, как изменится матрица квадратичной формы в результате линейного преобразования (3.32), подставим (3.32) в (3.31): (свойство 5 умножения матриц)(свойство 2 умножения матриц и равенство (3.33)) – матрица новой квадратичной формы.

Так как в “новой” системе координат кривая должна задаваться каноническим уравнением, то есть в нем должно отсутствовать произведение координат , тоимеет вид: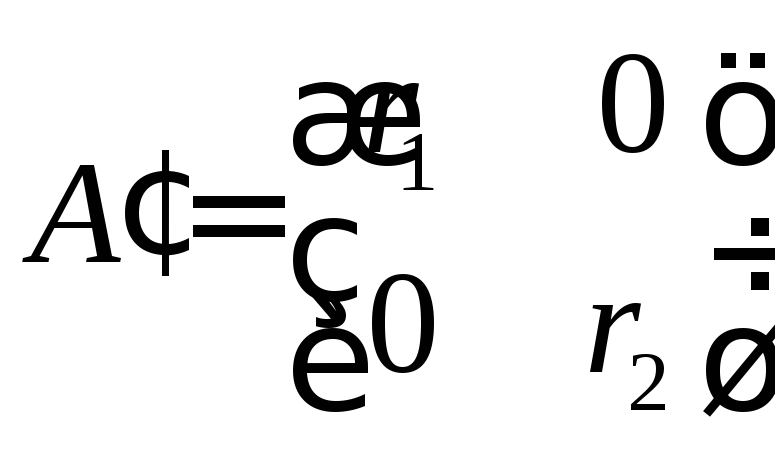, где– неизвестные числа. Умножим равенствона матрицуслева. Так как, то получим:

.

По определению равных матриц имеем:

, (3.34)

. (3.35)

Системы уравнений (3.34), (3.35) – линейные и однородные. Они имеют нетривиальное решение, если их определители равны 0.

.

Это означает, что иявляются решениями уравнения

. (3.36)

Уравнение (3.36) называется характеристическим уравнением матрицы (характеристическим уравнением квадратичной формы). Его решения иназываютсясобственными значениями матрицы (квадратичной формы).

Покажем, что дискриминант квадратного уравнения (3.36) положителен, то есть любая квадратичная форма двух переменных имеет 2 различных собственных значения.

Вычислим определитель (3.36):

.

Дискриминант ,

так как (иначе квадратичная форма будет канонической).

Таким образом, коэффициентами при ив каноническом виде квадратичной формы являются ее собственные значения, то есть решения уравнения (3.36).

Решим (3.36) и подставим в (3.34). Система имеет бесконечное множество решений и пусть– одно их них. Так как система (3.34) однородная, то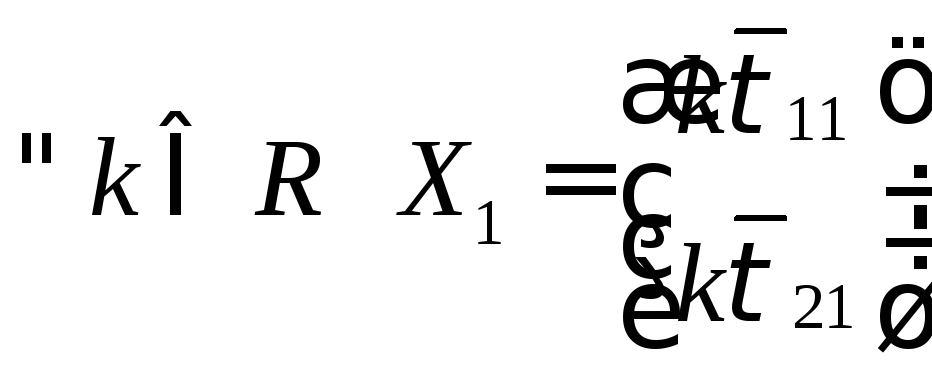– тоже решение. Подберемтак, чтобы векторбыл единичным:.

Векторы иназываетсясобственными векторами квадратичной формы, соответствующими собственному значению , илипервыми собственными векторами. Их направление называется первым главным направлением квадратичной формы. Таким образом, первым собственным вектором квадратичной формы называется любое ненулевое решение системы (3.34).

Аналогично подставим в (3.35) и найдем–второй собственный вектор, соответствующий собственному значению . Его направление называетсявторым главным направлением квадратичной формы. – второй единичный собственный вектор, то есть.

Можно показать, что . Кроме того,– первый собственный вектор, а– второй собственный вектор, поэтомуортами “новой” системы координат , к которой мы перейдем в результате линейного преобразования с матрицей,являются единичные собственные векторы квадратичной формы, найденные как решения систем (3.34), (3.35). Направив оси “новой” системы координат вдоль собственных векторов и, получим систему координат, в которой квадратичная форма будет иметь канонический вид.

ВЫВОД. Чтобы привести квадратичную форму к каноническому виду, надо:

1. Составить и решить характеристическое уравнение (3.36); его решения – собственные значения – являются коэффициентами при и в каноническом виде квадратичной формы.

2. Найти единичные собственные векторы, решив (3.34) и (3.35); они будут ортами новой системы координат . При этом если осьсонаправлена с, а ось– с, то– канонический вид, который квадратичная форма имеет в системе.